分数のたし算とひき算のやり方は？
通分の方法もわかりやすく解説

分数には「真分数・仮分数・帯分数」がある

分数には、真分数（しんぶんすう）、仮分数（かぶんすう）、帯分数（たいぶんすう）の3種類があります。

■真分数・仮分数

真分数とは、分子が分母より小さい分数のことです。例えば「1/4」や「3/4」は真分数にあたります。仮分数とは、分子が分母と等しいか、分子が分母より大きい分数のことです。例えば「4/4」や「6/4」は仮分数にあたります。

■帯分数

帯分数とは、整数と真分数を合わせた分数のことです。「1と2/4」のように、整数の横に真分数がついた形で表します。仮分数と帯分数は同じ大きさを表すことができ、互いに変換可能です。

■帯分数を仮分数に直す場合

例えば「2と4/5」という帯分数は、「14/5」という仮分数に直すことができます。仮分数に直したときの分子は、帯分数の分母×整数部分の数に、分子をたすことで求められます。

■仮分数を帯分数に直す場合

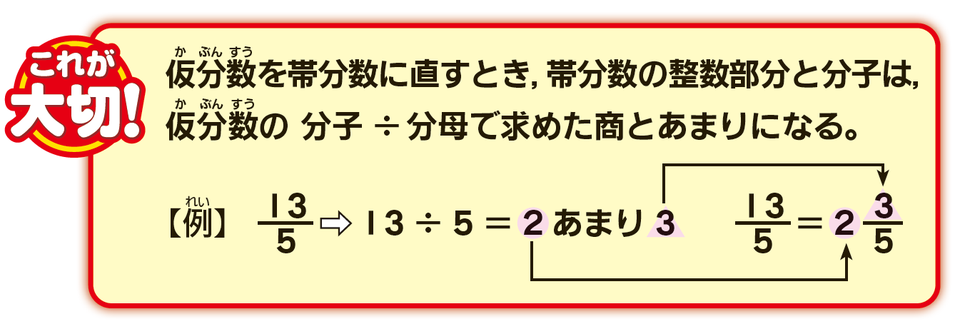
例えば「13/5」という仮分数は、「2と3/5」という帯分数に直すことができます。帯分数の整数部分は、仮分数の分子÷分母で求めた商になり、帯分数の分子はあまりの数になります。

真分数のたし算・ひき算のやり方

小学校3年生で学習するのは、分母が同じ真分数のたし算とひき算です。

分母が同じ真分数のたし算は、分子だけを計算することで答えが求められます。例えば「3/5＋1/5」という問題なら、「4/5」が答えです。しかし、分母もたして「4/10」と答えてしまうまちがいが多く見られます。

お子さまがこのようなまちがいをしてしまう場合には、分子が「1」の単位分数「1/5」をもとにして、「3/5は1/5の何個分か？」を考えるように伝えましょう。そのうえで、「3/5と1/5を合わせると、1/5の何個分になるか？」を考えれば、分子だけをたして答えを出すイメージが掴めます。

■分子が「1」の単位分数「1/□」をもとに何個分か考える例

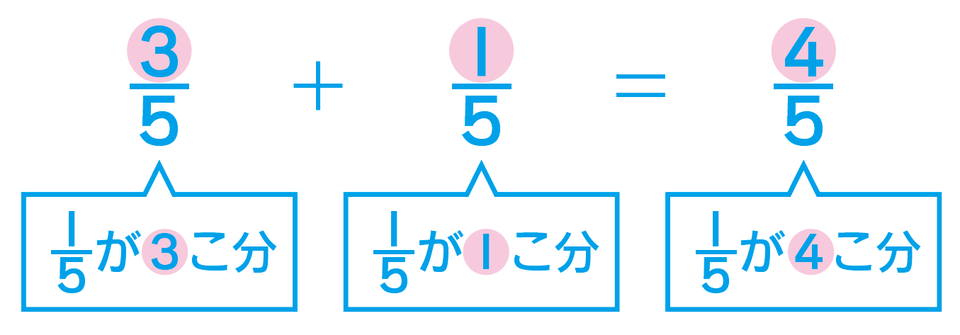
分母が同じ真分数のひき算も、分子だけを計算することで答えが求められます。例えば、「5/7ー3/7＝2/7」であれば、分子は「５－３＝2」となり、答えは2/7です。

帯分数のたし算・ひき算のやり方

小学校4年生で学習するのは、分母が同じ帯分数のたし算・ひき算です。

分母が同じ帯分数のたし算は、整数部分と分数部分に分けて計算することで求められます。分母の数字は変わりません。例えば「1と3/5＋2と1/5」の場合、整数部分は「1＋2＝3」、分数部分は「3/5＋1/5＝4/5」となり、答えは「3と4/5」です。「8/5＋11/5＝19/5」というように、帯分数を仮分数に直して計算することもできます。

分子部分を計算したら、分子が分母と等しいか、分母より大きくなった場合（仮分数になった場合）には、整数部分にくり上げて、帯分数に直す必要があります。

■帯分数に直す必要があるまちがい例

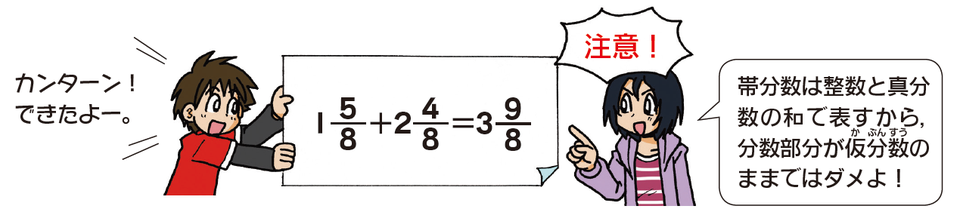
例えば、「1と5/8＋2と4/8」を計算した場合、答えを「3と9/8」とするのはまちがいです。帯分数は、整数と真分数（分子が分母より小さい分数）の和で表すものなので、仮分数の部分を真分数に直す必要があります。整数部分に1くり上げて、答えは「4と1/8」です。

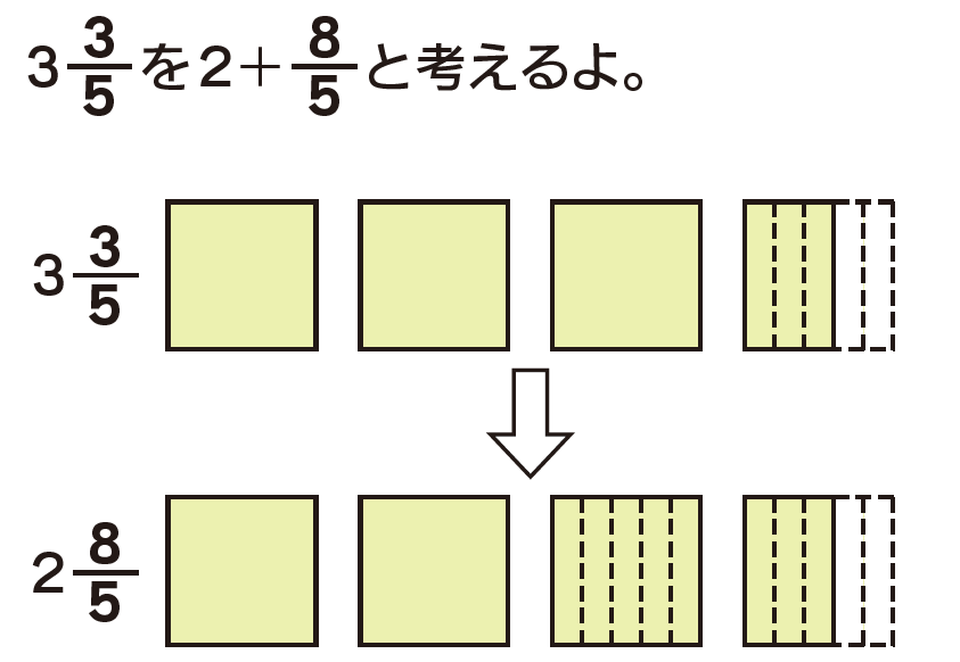
分母が同じ帯分数のひき算についても、整数部分と分数部分に分けて計算します。しかし、「3と3/5－1と4/5」のように、分数部分が「3－4」となり、ひき算できない場合があります。この場合は、ひかれる数の整数部分から1くり下げることが必要です。具体的には、「3と3/5」を「2と8/5」として、「2と8/5－1と4/5」、答えは「1と4/5」となります。

■ひかれる数の整数部分から1くり下げる例

「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」なら、分数のたし算・ひき算についてわかりやすいアニメーション解説で考え方を理解しながら、さまざまな問題に取り組めるので、分数の計算のつまずきを解消できます。学習履歴から苦手な問題を自動でピックアップしてくれるため、まちがえやすい帯分数のくり上げやくり下げについても、効率良く繰り返し学習できます。

分母がちがう分数のたし算・ひき算のやり方

分母がちがう分数を計算するには、分母が同じ分数に直す必要があります。これは「通分（つうぶん）」といって、小学校5年生で学習する単元です。分母がちがう分数のたし算・ひき算でつまずいてしまうお子さまは少なくありません。しっかり理解するためのポイントを見ていきましょう。

大きさの等しい分数はいくつでも作ることができる

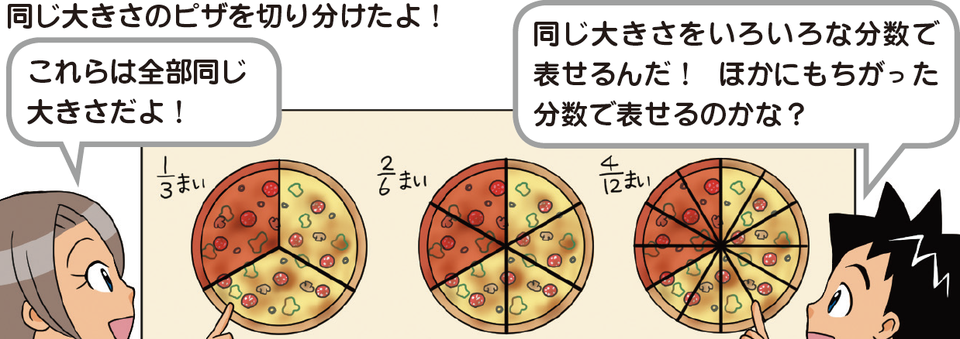
大きさの等しい分数は、いろいろな数で表すことができます。例えば、同じ大きさのピザを切り分けた場合で考えるとわかるように、「1/3」と「2/6」と「4/12」は大きさの等しい分数です。

■同じ大きさのピザを切り分けた場合

「1/3」の分母と分子に2をかけると「2/6」に、4をかけると「4/12」になります。反対に考えて、「2/6」の分母と分子を2でわると「1/3」に、「4/12」を4でわると「1/3」です。分母と分子に同じ数をかけても、分母と分子を同じ数でわっても、分数の大きさは変わりません。大きさの等しい分数はいくつでも作れることを理解しましょう。

分母を同じにする方法は「通分」

分母がちがう分数を、分母が同じ分数に直すことを「通分」といいます。通分して分母を同じにすることで、分数のたし算・ひき算ができるようになります。通分は、分数の分母と分子に同じ数をかけても、分数の大きさは変わらないという性質に基づいた考え方です。

■通分の方法

通分するときは基本的に、計算する分母の最小公倍数を共通の分母にします。例えば「3/5＋4/7」の場合、分母の5と7の最小公倍数である35を見つけて共通の分母にし、分子に分母と同じ数をかけます。

通分することで、「21/35＋20/35」という分数に直すことができ、たし算・ひき算ができるようになるのです。分母がちがう帯分数のたし算・ひき算の場合は、整数部分はそのままで、分数部分だけを通分します。

最小公倍数の見つけ方

通分して分母を同じにするためには、最小公倍数を見つける必要があります。最小公倍数を見つけるには、先に分母が大きいほうの倍数を書き出して、小さいほうの分母でわり切れる数を探すのがポイントです。

例えば「3/5＋4/7」の場合、まず大きいほうの7の倍数を考えていきます。7の倍数は、7・14・21・28・35・42…。小さいほうの5で最初にわり切れる数は35なので、35が最小公倍数だとわかります。

分数の基本をおさえて、たし算・ひき算の苦手を克服しよう

分数のたし算とひき算においては、分数の性質をしっかりと理解することが大切です。分数は「1つのものを同じ大きさに分けたうちのいくつ分か」を表す数であるとわかれば、分母が同じ場合なら、分子だけを計算すればいいことがわかります。

また、「分母と分子に同じ数をかけても分数の大きさは変わらない」ことがわかれば、分母がちがう分数を通分して計算できます。分数の性質をおさえつつ問題演習を重ねることで、分数のたし算・ひき算のつまずきを解消しましょう。

「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」なら、分数のたし算・ひき算のさまざまな問題をくり返し学習することができます。まちがえた直後に解き直しができるため、理解がその場で深まり、苦手をそのままにせずきちんと解消できるのが特長です。短い時間でも集中して取り組める設計で、お子さまが毎日コツコツ続けやすい工夫がたくさん詰まっています。家庭学習の習慣づけにもつながる「進研ゼミ小学講座」で、算数の力を伸ばしましょう。