- 学習法
立体の体積の求め方は?
つまずきやすいポイントをわかりやすく解説

立体の体積は、小学校高学年になると学習する算数の重要な単元のひとつです。しかし、公式や実際の計算の理解ができていなかったり、複雑な立体になると求め方がわからなくなってしまったりすることも少なくありません。
この記事では、立方体や直方体をはじめとした基本的な立体や複雑な形の立体の体積の求め方、そして、つまずきやすいポイント、さらにご家庭でできる学習サポート方法を解説します。
<目次>
立体の体積とは?
立体の体積とは、もののかさのことです。体積の単位には、立方センチメートル(cm³)や立方メートル(m³)などが使われ、三次元空間における立体の大きさを表現します。二次元である平面の面積とは異なり、高さや深さを含むため、理解に時間がかかるお子さまも少なくありません。
面積と体積の違い
面積は、例えば縦×横で長方形の面積が求められるように、縦と横の二方向の広がりで平面上の広さを表す量です。一方で体積は、縦、横、高さの三方向の広がりを持つ立体の大きさを示す量です。面積の単位が2つの長さをかけたことを表す平方センチメートル(cm²)であるのに対し、体積は3つの長さをかけたことを表す単位の立方センチメートル(cm³)を使用します。
このように、面積と体積では「次元」が異なることを認識できていない子どもたちにとっては、混同しやすい傾向がみられます。しっかりと違いを理解することが、体積の学習において重要です。
小学生の図形の学習
「文部科学省」の学習指導要領によると、小学1年生から3年生までは「図形領域」と「測定領域」に分かれて学習が進み、4年生から「測定領域」が「図形領域」に統合され、立体的な図形の理解が求められるようになります。5年生では、いよいよ体積の単元が登場し、6年生になると「底面積×高さ」という公式を用いて計算します。
4年生で学習する面積や長さ、単位の関係性をしっかり理解していないと、体積の単元でつまずいてしまうかもしれません。また、体積の学習は中学校の学習にもつながるため、小学生のうちに土台をしっかりと築いておくことが重要です。
小学校で習う立体の種類と体積を求める公式
小学校で学習する立体の体積は、主に「立方体」「直方体」「角柱」「円柱」の4種類です。これらの立体にはそれぞれの特徴があり、体積を求めるための式も異なります。まずは、これらの立体の基本的な形と公式を確認しておきましょう。
| 種類 | 形 | 公式 |
|---|---|---|
| 立方体 | 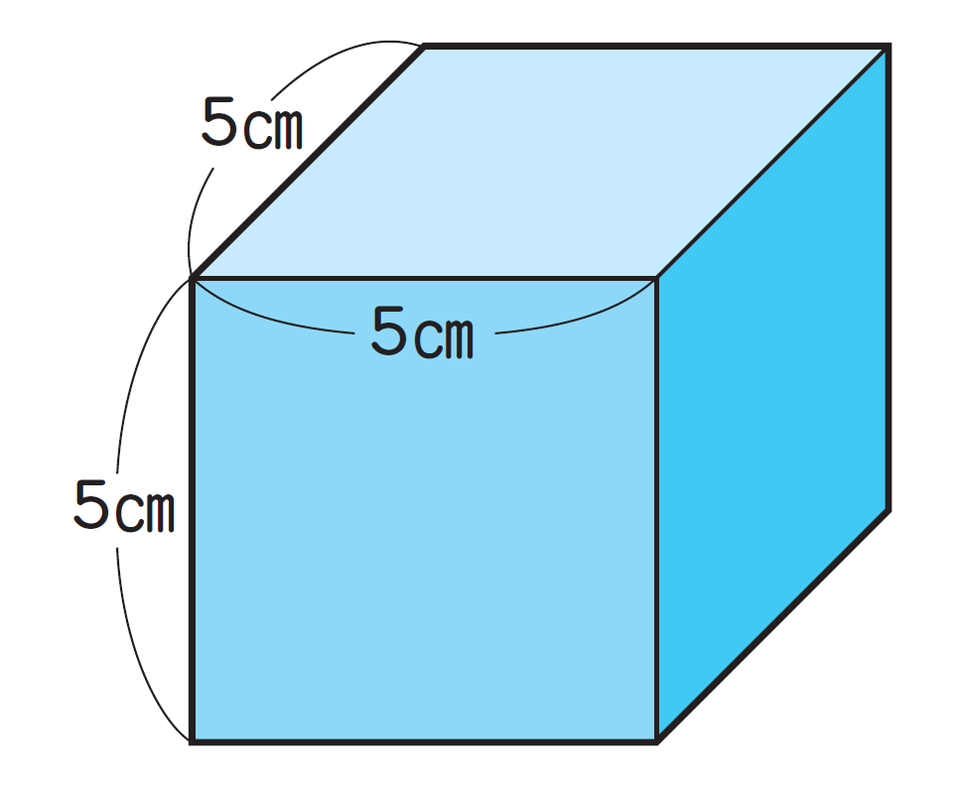 |
立方体の体積=1辺×1辺×1辺 |
| 直方体 | 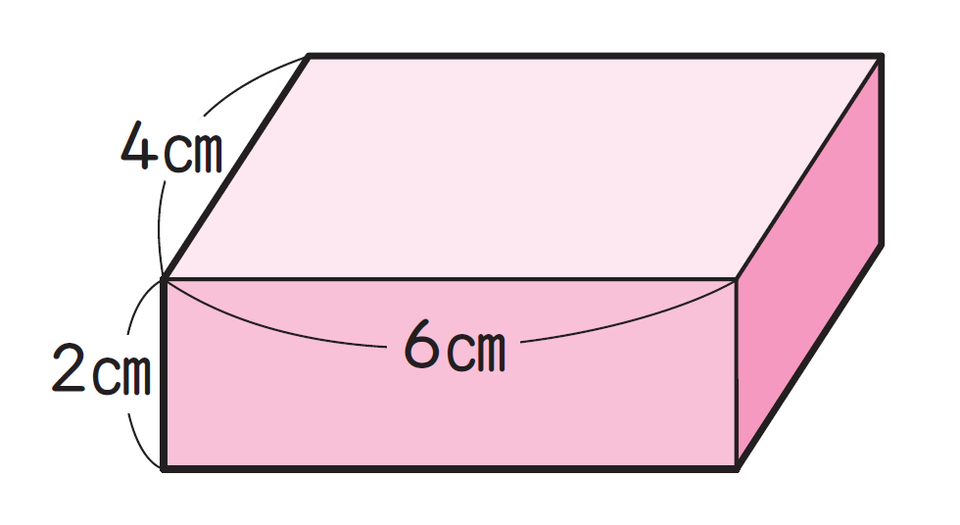 |
直方体の体積=縦×横×高さ |
| 角柱 (例:三角柱の場合) |
 |
三角柱の底面積=底辺×高さ÷2 三角柱の体積=底面積×高さ |
| 円柱 | 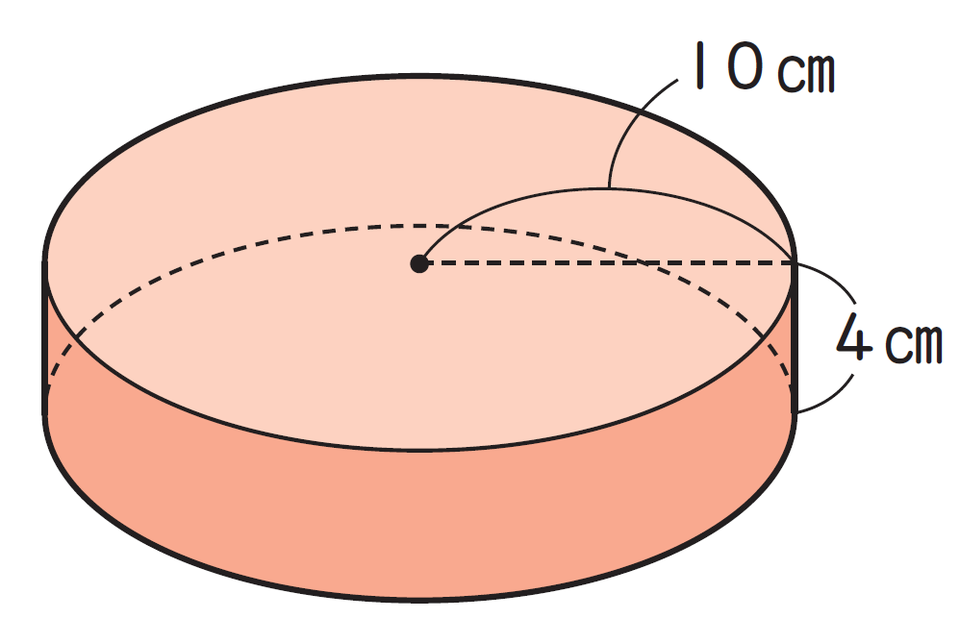 |
円柱の底面積=半径×半径×3.14 円柱の体積=底面積×高さ |
上記の公式を覚えるだけでなく、どの部分を用いて計算するかといった立体の構造をしっかり理解することが重要です。とくに三角柱や円柱は、底面積の求め方が複雑で混乱しやすいため、しっかり確認しておきましょう。
ここからは、各立体の特徴と計算例を解説していきます。
<各立体の特徴と計算例>
- 立方体
- 直方体
- 三角柱
- 円柱
立方体
立方体とは正方形だけで囲まれた形で、縦・横・高さのすべての長さが等しい箱のような形をした立体です。サイコロや積み木など、身近にも多くの立方体の形が存在します。立方体では、縦・横・高さのすべてが同じ長さのため、「縦」「横」「高さ」という言い方ではなく「1辺」という言い方をします。
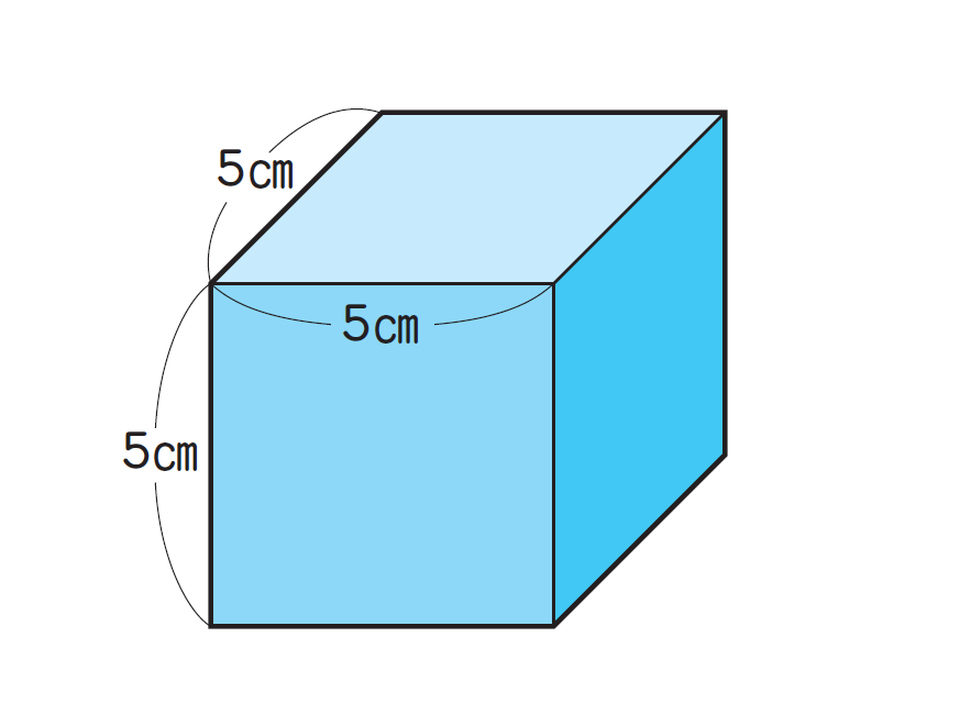
<例題>
上記の立方体の体積は何立方センチメートル(cm³)ですか?
<式>
5×5×5=125
<答え>
125cm³
<解説>
立方体の体積の求め方は非常にシンプルで、「体積=1辺×1辺×1辺」の公式を使います。この公式を理解するためには、「1辺が1cmの立方体が、何個分集まってできているのか」という視点が重要です。立方体の形をした積み木などを使って、実際に立方体を作りながら学習すると、理解が深まりやすくなります。
直方体
直方体は長方形だけ、または長方形と正方形で囲まれた形で、たて・よこ・高さに異なる長さがある長方形の箱のような形をした立体です。ティッシュ箱や豆腐など、日常生活の中でもよく見られる形です。
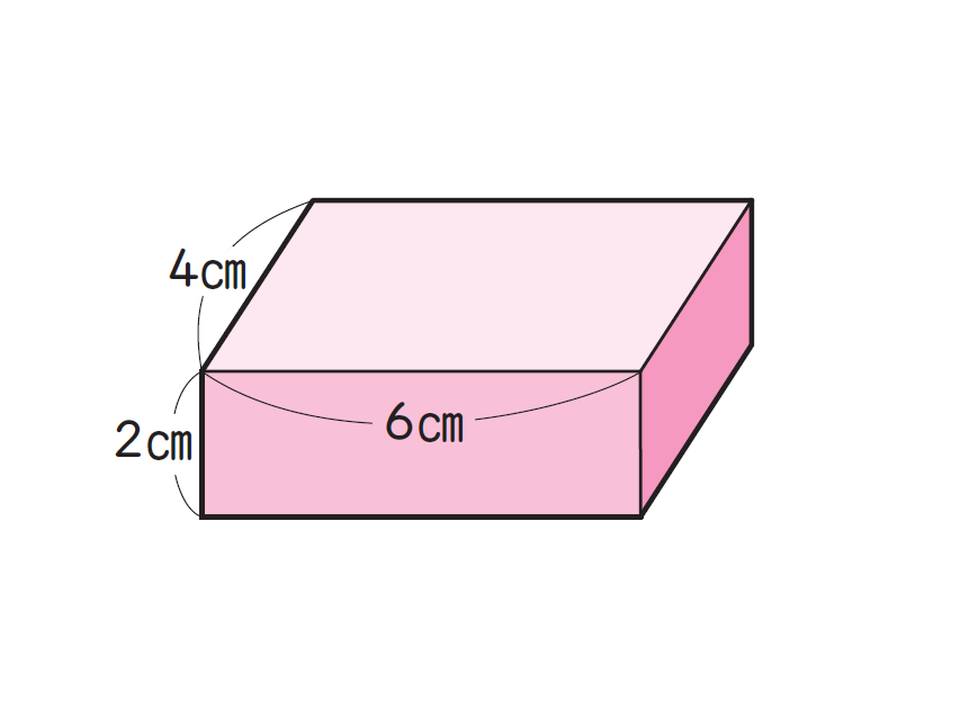
<例題>
上記の直方体の体積は何立方センチメートル(cm³)ですか?
<式>
4×6×2=48
<答え>
48 cm³
<解説>
直方体の体積を求める公式は、「体積=たて×よこ×高さ」です。立方体との違いは、「辺の長さに異なるものがある」ことにあります。お子さまには、立方体との違いを意識しながら、どの辺が「たて」「よこ」「高さ」にあたるのかを整理して式に表すようにさせると、より正確に理解できます。
角柱(例:三角柱の場合)
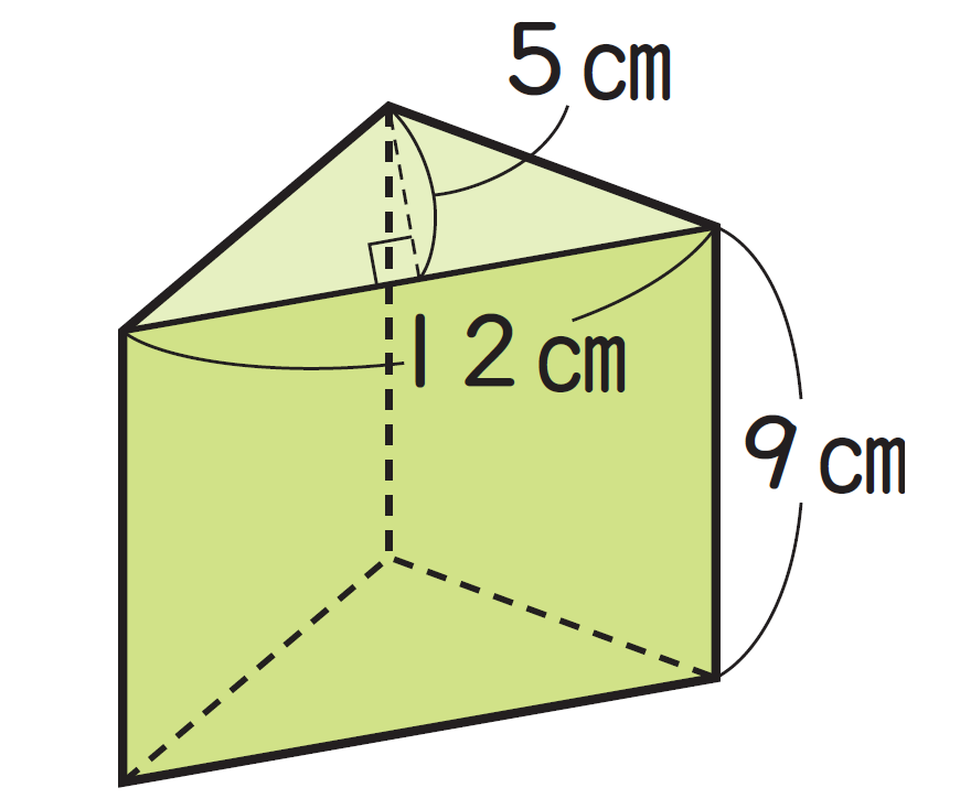
三角柱とは、同じ形で同じ大きさの三角形の底面が2つ上下に向かい合っていて、まわりの面は縦の長さが等しい長方形や正方形になっている立体のことを指します。見慣れない形のため、混乱しやすい立体のひとつです。三角柱のまわりの面のことを「側面」といい、側面の縦の長さを三角柱の「高さ」といいます。
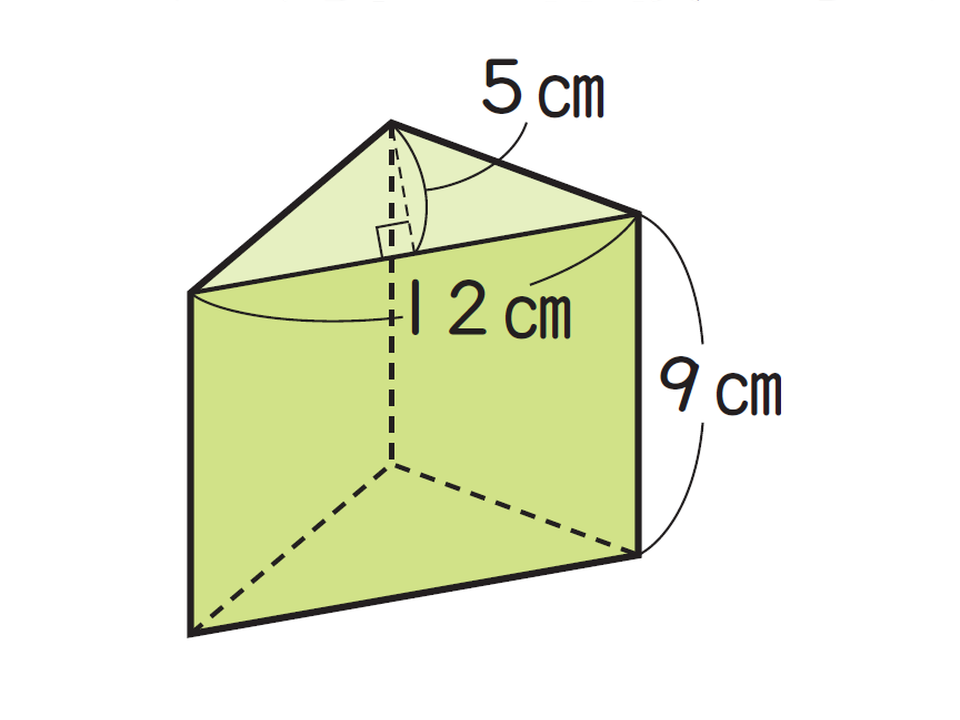
<例題>
上記の三角柱の体積は何立方センチメートル(cm³)ですか?
<式>
12×5÷2=30
30×9=270
<答え>
270 cm³
<解説>
角柱の体積を求める公式は、「体積=底面積×高さ」です。三角柱の場合、「底面積」とは底面である三角形の面積のことで、「底辺×高さ÷2」の式で求めたあとに、その面積に三角柱の高さをかけて体積を求めます。
計算手順が2段階になるため、ミスが起こりやすいポイントでもあります。お子さまには、底面積の求め方と、体積計算の2ステップを分けて丁寧に指導することが大切です。
円柱
円柱は、上下に同じ大きさの円の底面を持ち、高さがどこも等しい側面でぐるっと囲まれた筒状の形をした立体です。缶ジュースや水筒などが円柱の例です。
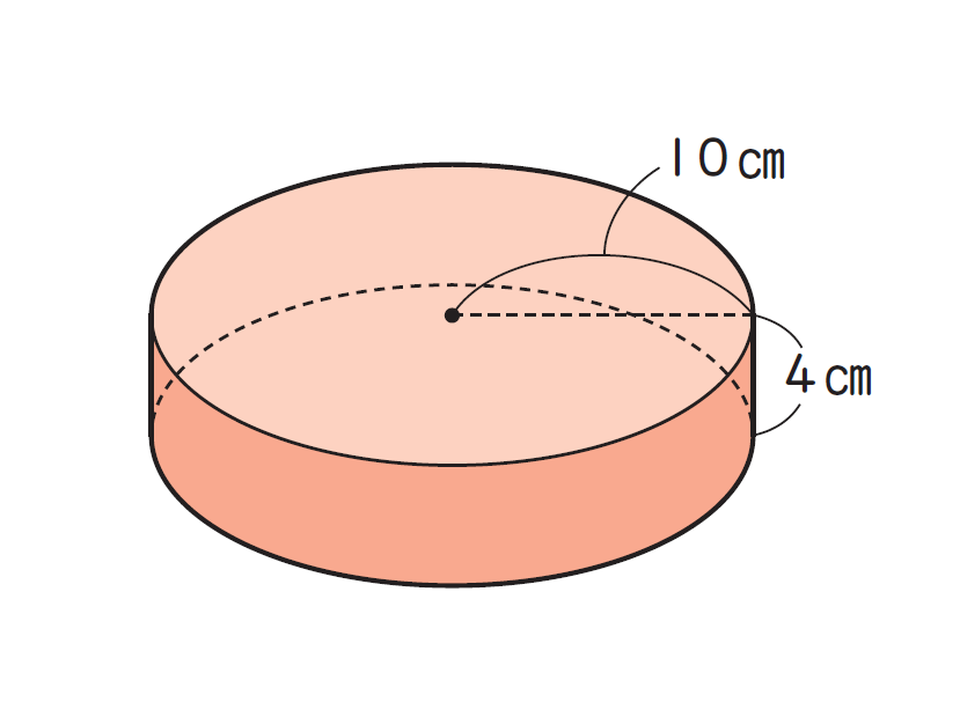
<例題>
上記の円柱の体積は何立方センチメートル(cm³)ですか?
<式>
10×10×3.14=314
314×4=1256
<答え>
1256 cm³
<解説>
円柱の体積も、「体積=底面積×高さ」で求められます。しかし、底面が「円」なので、「底面積=半径×半径×円周率」を用いて計算するのがポイントです。
たとえば上記の場合は、半径10cm、高さ4cmの円柱なので、まず底面積を「10×10×3.14=314」で求め、次に体積を「314×4=1256」と求めます。
【応用問題】複雑なかたちの立体の体積
5年生では、直方体と立方体の体積の求め方を学習したあと、下記のような複雑な形の立体の体積の求め方を学習します。
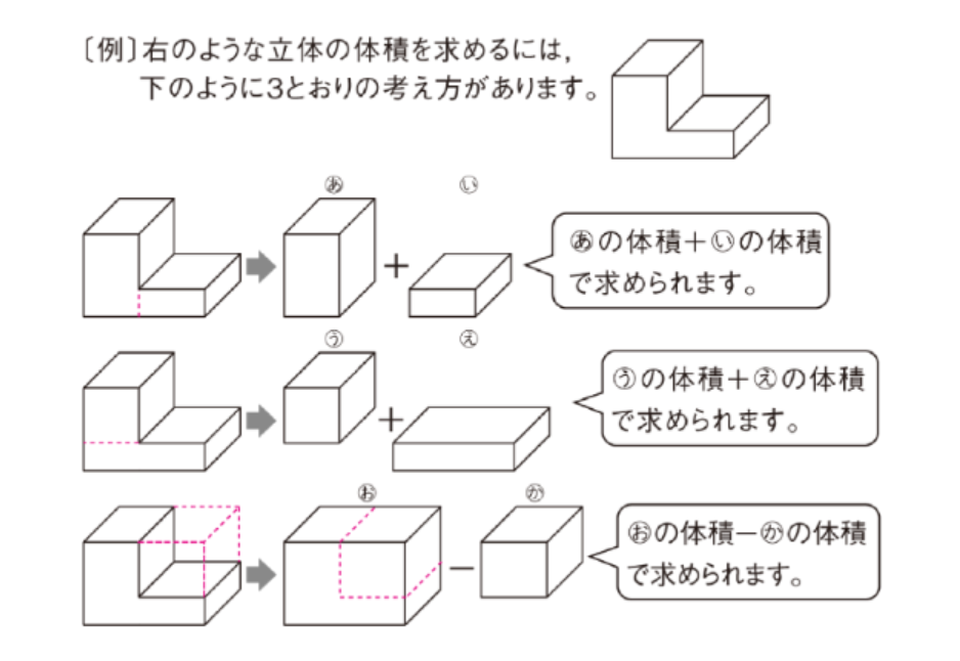
実際に5年生の応用問題にチャレンジしてみましょう。ここでは、上記のような複雑なかたちの立体の体積の求め方や考え方を紹介します。

<例題>
上記の立体の体積は、何立方センチメートル(cm³)ですか?
<式>
10×11×6=660
10×5×2=100
660+100=760
<答え>
760 cm³
<解説>
複雑なかたちの体積を求める場合、直方体の体積の公式が使えるように立体を分けて考えることで求められます。上記の式は、以下のように(あ)と(い)に分けて求めた例です。
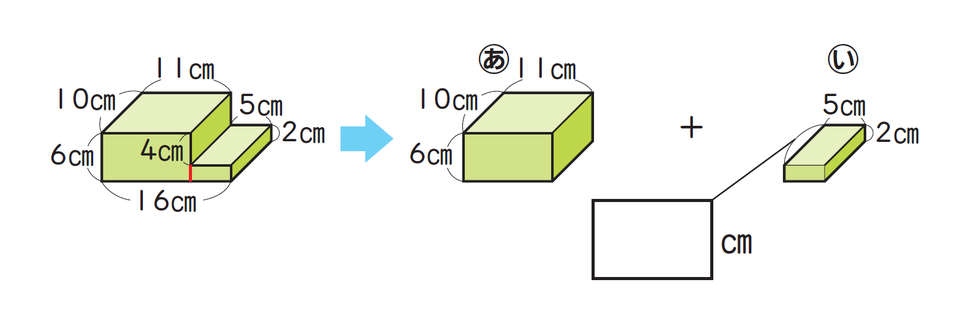
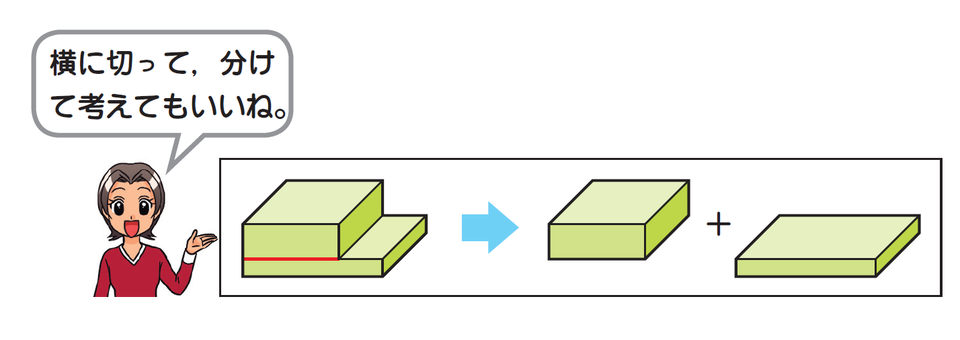
ただしこの分け方は一例であり、複雑なかたちの立体はさまざまな分け方・考え方ができます。たとえば、以下のように立体を横に切り、それぞれの直方体の体積を求めてたしても同じ答えになります。
また、大きい直方体から欠けている部分の直方体を取り除いた形だと考えて、「大きい直方体の体積-欠けている部分の直方体の体積」で求めることもできます。
立体の体積を求める際につまずきやすいポイント
立体の体積の学習では、立体の体積を求める公式を覚えるだけでなく、その意味や使い方を正しく理解することが大切です。ここでは、小学生が立体の体積を求める際によくあるつまずきポイントを紹介します。
<立体の体積を求める際につまずきやすいポイント>
- 答えの単位の誤り
- 図形と式の意味の関連づけが弱い
答えの単位の誤り
体積の単位は、立方センチメートル(cm³)や立方メートル(m³)などが使われますが、面積で使う平方センチメートル(cm²)や平方メートル(m²)と混同しやすく、答えの単位で間違えるケースが多く見られます。こうした単位の違いと立体の体積を求める考え方を視覚的・体感的に理解させることが重要です。
図形と式の意味の関連づけが弱い
公式を暗記していても、「なぜその式になるのか」が理解できていないと、応用問題などに対応できません。特に「底面積×高さ」という式の意味を図形と結びつけて理解していないと、式に当てはめるだけで終わってしまい、誤答の原因になります。このような場合、積み木や立体モデルを使って、図形と式の意味をつなげる経験を積むことが効果的です。
家庭でできる学習サポート
立体の体積は、式だけで理解するのが難しい単元のひとつです。ご家庭での学習サポートでは、できるだけ実物にふれながら、体積の感覚や式の意味を体験として理解させることがポイントになります。ここでは、ご家庭で実践できる具体的な学習方法を3つご紹介します。
<家庭でできる学習サポート>
- 身近なものの体積を求める
- 積み木やブロックを使って量感を養う
- タブレット教材を活用する
身近なものの体積を求める
牛乳パックやティッシュ箱など、形が立方体や直方体に近い身近なものを使い、縦・横・高さを実際に計測して体積を求めてみてください。同じような体積でも、形が違うと見た目の印象が変わるため、量の感覚(量感)を身につけるのに役立ちます。また、複数のものを比べることで、「数値では同じでも形によって感じ方が違う」という気づきを得ることができるでしょう。
積み木やブロックを使って量感を養う
立方体の形をした積み木や立方体ブロックを使って直方体の形を作り、縦×横×高さで何個のブロックを使ったかを数えることで、体積を視覚的・体感的に学ぶことができます。ブロックを組み替えても、個数が同じなら体積も同じであるということを体験することで、「縦×横×高さ」の意味も自然と理解できるようになるでしょう。学習に苦手意識がある場合も遊び感覚で取り組めるため、抵抗なく学べるのがメリットです。
タブレット教材を活用する
立体の体積をアニメーションや図解で視覚的に解説してくれるタブレット教材は、立体の体積の理解を深めるのに効果的です。自分のペースで繰り返し学習できるうえ、ミスの原因もフィードバックしてくれるため、学習の質が高まります。
「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」なら、動画やアニメーションを用いてお子さまが一人でも楽しく取り組める設計になっています。詳細は以下より資料を請求できますので、ご確認ください。
つまずきやすい立体の体積は、家庭学習で理解を深めよう
立体の体積は、シンプルな公式で求められるものの、公式を覚えるだけでは応用問題に対応できないため、数値と形を結びつけて理解することが大切です。特に小学生にとっては、立体の分解・組み合わせといった場面でつまずきやすいため、実体験を通じた学びが欠かせません。
家庭学習では、牛乳パックなどのものを計測して体積を求めてみたり、積み木やブロックで体積を確かめてみたりすることで、量の感覚を養うことができます。また、タブレット教材を組み合わせることで、繰り返し学習と視覚的な理解が両立でき、苦手を効率よく克服することが可能です。
「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」なら、アニメーションや図形モデルを活用した解説や豊富な練習問題を通じて、お子さまが一人でも楽しく学べる環境が整っています。家庭学習の一環として上手に取り入れ、立体の体積の基礎をしっかりと固めていきましょう。
- ここでご紹介している教材・サービスは2026年2月現在の情報です。教材ラインナップ・デザイン・名称・内容・お届け月などは変わることがあります。