- 学習法
平行四辺形の面積の求め方は?
図形問題の学習ポイントを解説

平行四辺形の面積は「底辺×高さ」で求められることを知っていても、その公式の意味や使い方を正しく理解できていないお子さまは少なくありません。特に、教科書の図だけでは高さの捉え方があいまいになり、正しい面積を求められないこともあります。
この記事では、平行四辺形の面積を求める公式の理解や、高さの正しい見つけ方をわかりやすく解説します。また、家庭学習で図形問題の理解を効率的に深められる「進研ゼミ小学講座」の活用方法についても紹介するので、参考にしてください。
平行四辺形の定義と面積の定義
まずは、平行四辺形の底辺や高さなどの言葉の定義を理解しましょう。
平行四辺形は向かい合った2組の辺がそれぞれ平行になっている四角形
平行四辺形は、向かい合った2組の辺がそれぞれ平行になっている四角形のことです。上と下の辺が平行で、さらに左と右の辺も平行という特徴があります。この性質を理解すると、面積を求める際に高さの位置や形のバリエーションにも柔軟に対応できるようになります。
■平行四辺形は向かい合った2組の辺の長さがそれぞれ等しい四角形のこと
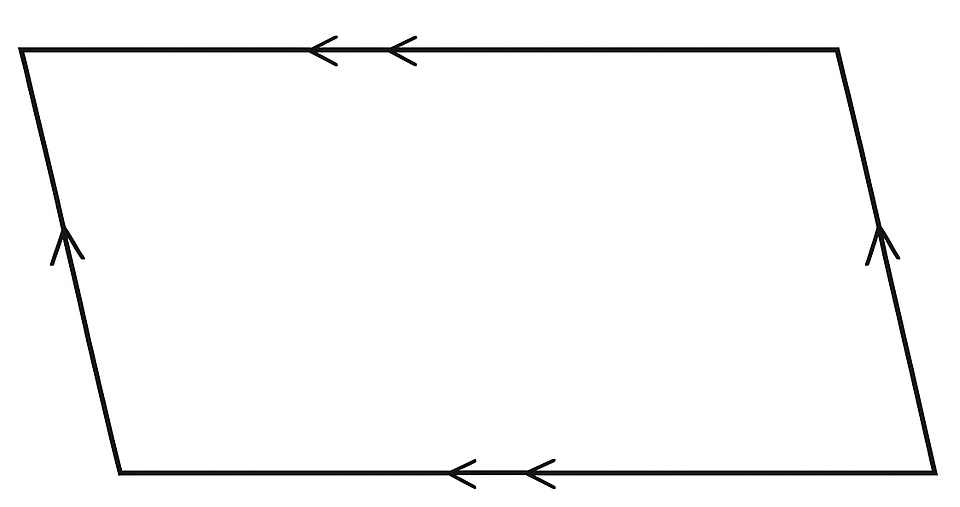
平行四辺形の高さは、底辺に垂直な直線の長さ
平行四辺形の高さは、選んだ底辺に対して垂直に引いた直線の長さを指します。高さは辺の長さそのものではなく、底辺と向かい合った辺との最短距離として測られます。
図によっては高さが図形の外側に位置する場合もあり、その場合は延長した底辺に垂直な線を引いて測ります。この高さの正しい位置と意味を理解することが、面積を正確に求めることにつながります。
■平行四辺形の高さ

平行四辺形の面積を求める公式
平行四辺形の面積を求める公式は、次のとおりです。
■平行四辺形の面積を求める公式

<例題>
次の平行四辺形の面積を求めましょう。
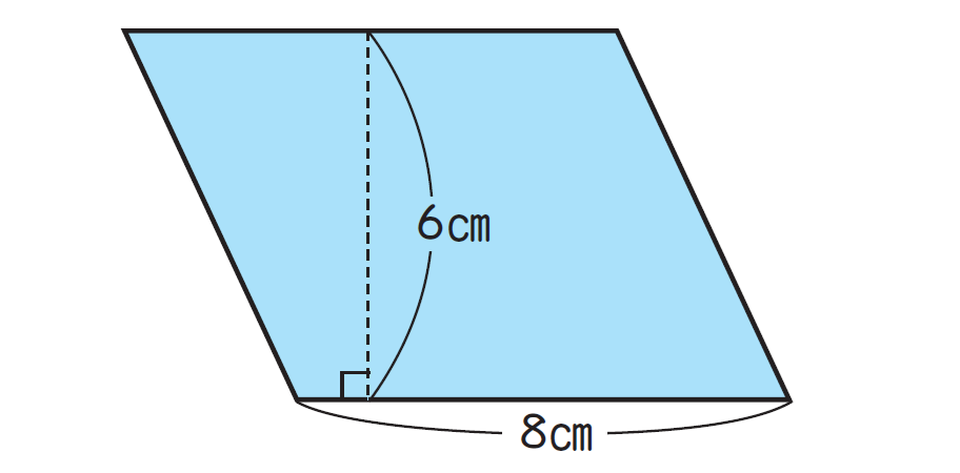
<式>
8×6=48
<答え>
48cm²
高さはななめの辺ではなく、底辺に対して垂直の直線を指します。この問題では底辺8cmに対して、垂直な線、つまり高さは6cmです。したがって、公式にあてはめて計算すると48cm²となります。答えには必ず面積を表す単位をつけましょう。
<例題>
次の平行四辺形の面積を求めましょう。
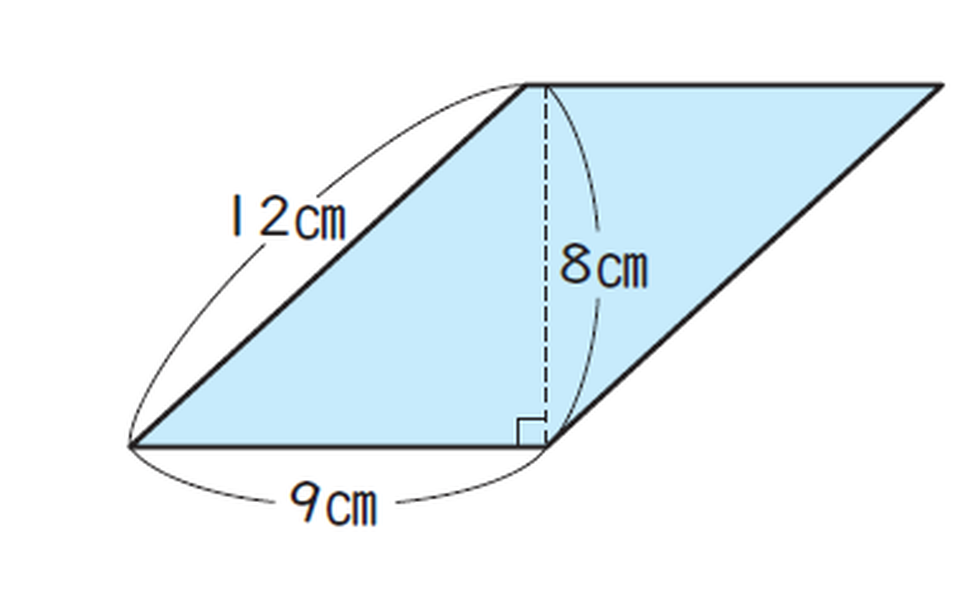
<式>
9×8=72
<答え>
72cm²
この問題では、12cmの辺は底辺に対して垂直ではないので、高さではありません。底辺を9cm、高さを8cmとして公式にあてはめて計算し、面積を求めます。お子さまにはヒントとして「底辺に対して垂直な線はどれかな?」などと声かけをし、高さにあたる線を探すのがポイントです。
<例題>
次の平行四辺形の面積を求めましょう。
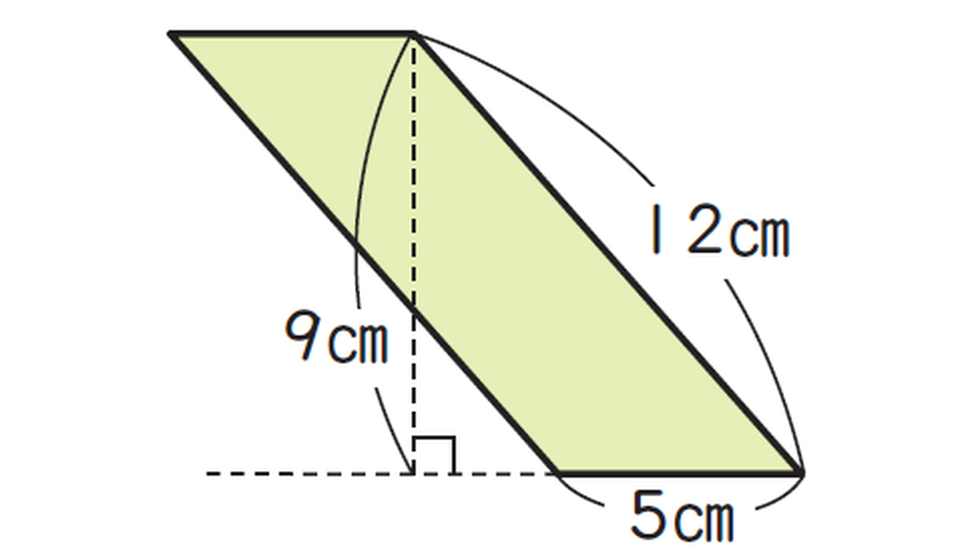
<式>
5×9=45
<答え>
45cm²
この問題では、底辺が5cm、高さが9cmです。12cmの辺は底辺に対して垂直ではないので、高さではありません。高さの表示が平行四辺形の中にあるか外にあるかは関係ないので注意してください。
平行四辺形の面積の求め方を教えるポイント
平行四辺形の面積を学ぶときは、公式を覚えるだけでなく、日常生活とのつながりを感じられる工夫が欠かせません。例えば、屋根や床のタイル、カバンの模様など、生活の中にある平行四辺形をおうちのかたもいっしょに探してみましょう。身近な例と結びつけることで、「算数=実生活に役立つ」という実感が湧き、お子さまの学習意欲も高まります。
また、図に数値を書き込むだけでなく、「面積がどのくらいになるのか」「単位は何を使うのか」といった点までおうちのかたがいっしょに考えれば、数字の意味を理解しやすくなります。
おうちのかたが忙しい場合は、「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」での学習がおすすめです。タブレットがその日に学ぶ課題を自動で提示してくれるので、迷わず家庭学習に取り組めます。面積などの難しい単元も、アニメーション解説でわかりやすく理解できるため、お子さま一人でも楽しく学習可能。教材やサポートが充実しており、学習の定着をしっかり後押しします。無料体験でぜひお試しください。
平行四辺形に関する応用問題
平行四辺形の面積を求める問題について、応用問題を見ていきましょう。
<例題>
次の平行四辺形の面積を求めましょう。
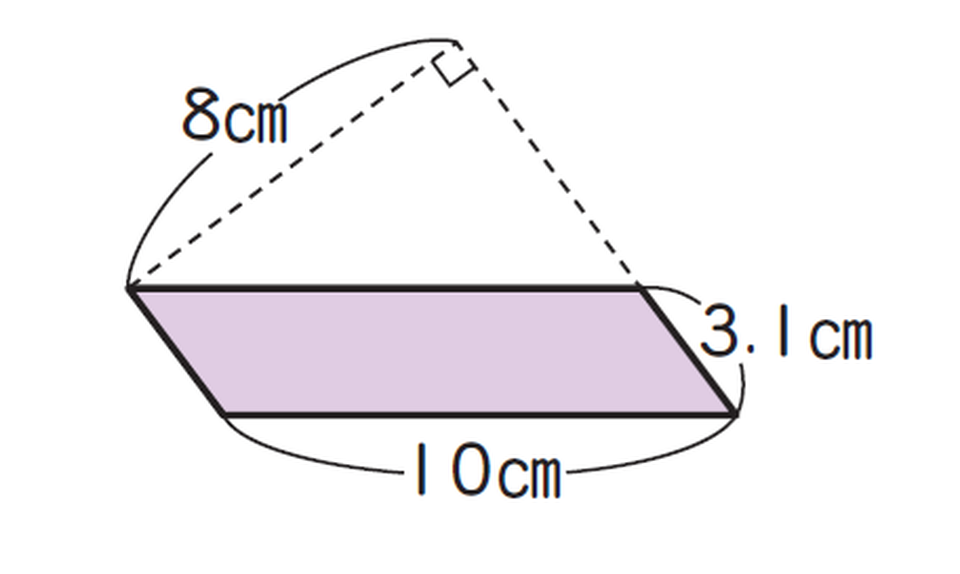
<式>
3.1×8=24.8
<答え>
24.8cm²
直角のマークに注目すると、3.1cmが底辺、8cmが高さとなります。10cmの辺は今回の計算では使わないので注意が必要です。
平行四辺形の面積と底辺から、高さを求める問題も見てみましょう。
<例題>

わかっている数字を確認し、求めたい高さは「□」として、平行四辺形の面積を求める公式にあてはめます。
<式>
5×□=30
(底辺×高さ=面積)
30÷5=6となり□に当てはまる数は6のため、高さは6cmであることがわかります。
<答え>
6cm
算数の図形学習の土台づくりには「進研ゼミ小学講座」がおすすめ
算数の図形問題は、一度つまずくと「算数=苦手」という気持ちが芽生えてしまうお子さまも少なくありません。お子さまが図形問題に苦手意識を持つことなく取り組むようになるには、自分から「やってみたい」と思える工夫と環境づくりが必要です。そのためには、ご家庭での声かけや学習の工夫が、継続のカギになります。
特に、お子さまに合った教材選びは重要です。楽しく続けられる教材であれば、図形への苦手意識が減り、日常的に学びが根づいていくでしょう。
専用タブレットを使う「進研ゼミ小学講座」の「チャレンジタッチ」なら、お子さまの理解度やペースに合わせて、毎日の学習プランを自動で提案。図形問題もアニメーションや図解、ミニゲームなどで視覚的に学べるので、つまずきがちな面積の求め方も自然と身につきます。直感的な操作で、小学生でも自分で進めやすい設計です。
家庭学習で図形の力をつけたいなら、「進研ゼミ小学講座」の「チャレンジタッチ」を活用して、楽しみながら理解につなげてみてはいかがでしょうか。
- ここでご紹介している教材・サービスは2026年1月現在の情報です。教材ラインナップ・デザイン・名称・内容・お届け月などは変わることがあります。