- 学習法
長方形の面積と横の長さから、
たての長さはどう求める?

子どもが算数の「長方形の面積」でつまずいたとき、どのように教えたらよいか悩む保護者のかたも多いでしょう。長方形の面積は「たて×横」で求められますが、「面積と横の長さ」から「たての長さ」を求める問題では、考え方が逆になるため混乱しやすくなります。
この記事では、長方形の面積を求める発展問題を解説するほか、「進研ゼミ小学講座」の「チャレンジタッチ」を使った効果的な学習法についても紹介します。
<目次>
長方形の面積を求める公式
長方形の面積を求める公式はとてもシンプルです。正方形の面積を求める公式といっしょにおさらいしておきましょう。
■長方形・正方形の面積を求める公式

次の長方形の面積を求めましょう。
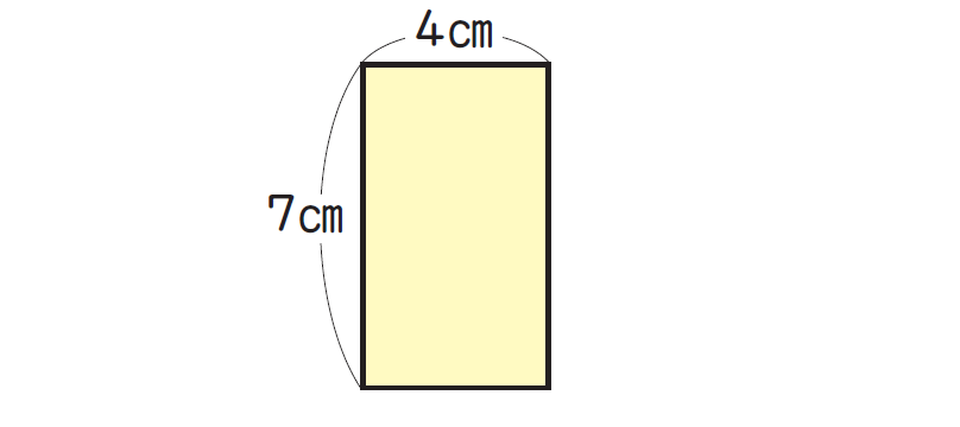
この長方形は、たてが7cm、横が4cmです。長方形の面積を求める公式にあてはめると、式と答えは次のようになります。
<式>
7×4=28
<答え>
28cm2
なお、かけ算は順序を入れ替えても結果が同じになるため、公式の順序は「たて×横」でも「横×たて」でも構いません。大切なのは、となり合った2つの辺の長さを表す数をかけると面積が求められることの理解です。順番を機械的に覚えるよりも、面積の意味を理解すれば、お子さまの納得感と応用力が高まるでしょう。
面積を表す単位のおさらい
面積を表す単位は、「cm²(平方センチメートル)」以外にもあります。計算をする際には、たて・横の長さの単位がそろっているか確認し、答えには必ず単位をつけなくてはいけません。また、問題文で登場する単位と答えで求められている単位が違う場合もあるので注意が必要です。
次の例題で考えてみましょう。
<例題>
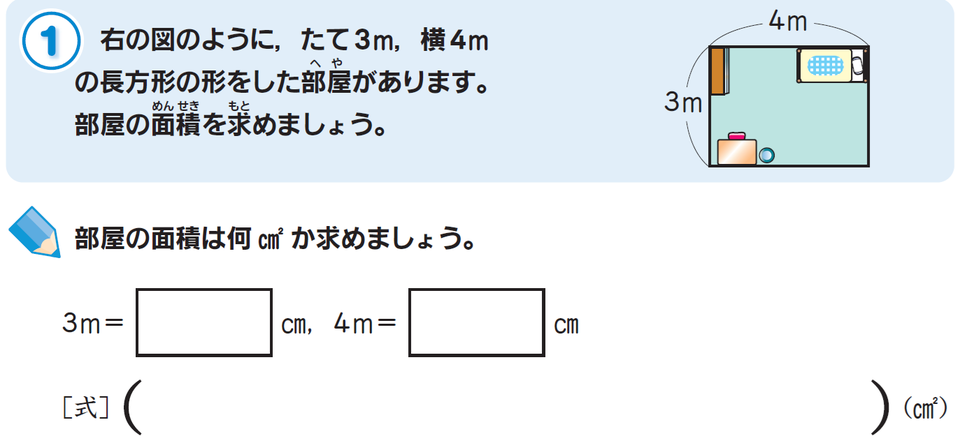
1m=100cmなので、3m=300cm、4m=400cmです。
<式>
300×400=120000
<答え>
120000cm²
このように問題と求められている答えで単位が異なることがあります。
もし「何㎡でしょう。」という問題だったらどうでしょうか。
㎠より大きな単位㎡(平方メートル)で考えてみましょう。

先ほどの部屋の面積が何㎡かを求めると、下記のとおりです。
<式>
3×4=12
<答え>
12㎡
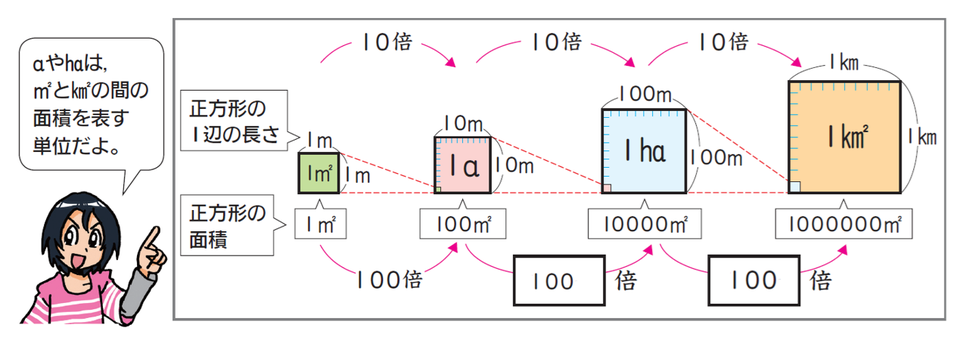
さらに大きな面積を表す単位に、a(アール)、ha(ヘクタール)、km²(平方キロメートル)があります。それぞれの単位の関係は下記のとおりです。
■㎡、a、ha、k㎡の関係
複雑な形の面積を工夫して求める方法
長方形の面積を求める公式が理解できたら、さらに複雑な図形の面積も工夫して求めることが可能です。次の例題で考えてみましょう。
<例題>

このような図形の面積を求める場合、公式を使えるように線をひいて、2つの長方形をつくります。この場合、考え方は2通りあります。

ここでは、たてに線をひいた場合で考えてみましょう。
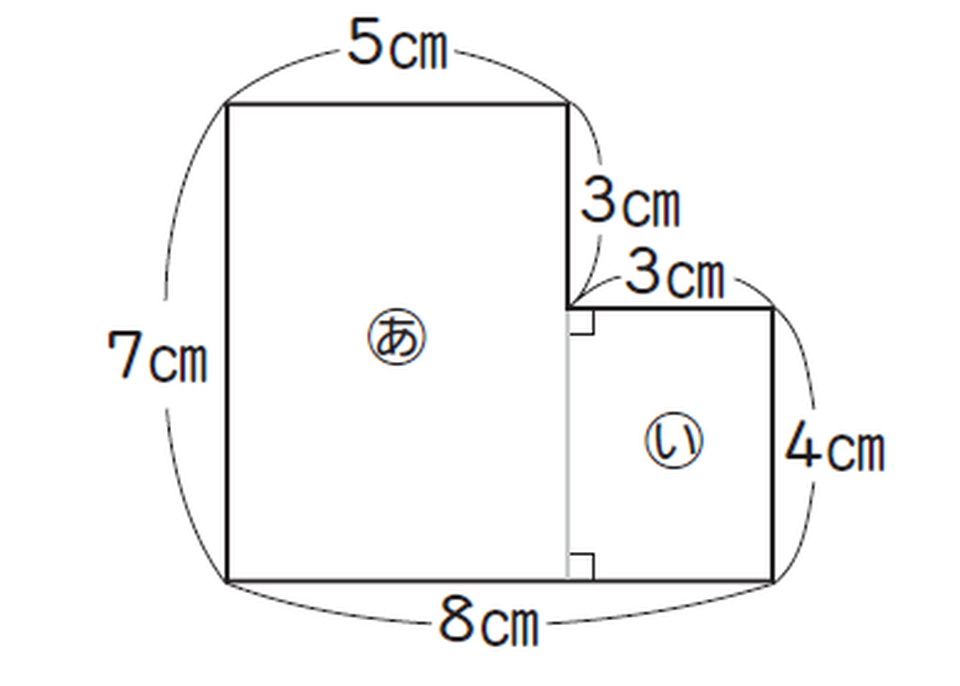
上の図のように線をひくと、2つの長方形ができます。それぞれの面積を計算してからたすと、全体の面積を求められます。
<式>
7×5+4×3=35+12=47
<答え>
47cm2
同様の考え方で、次のような問題も解くことが可能です。
<例題>
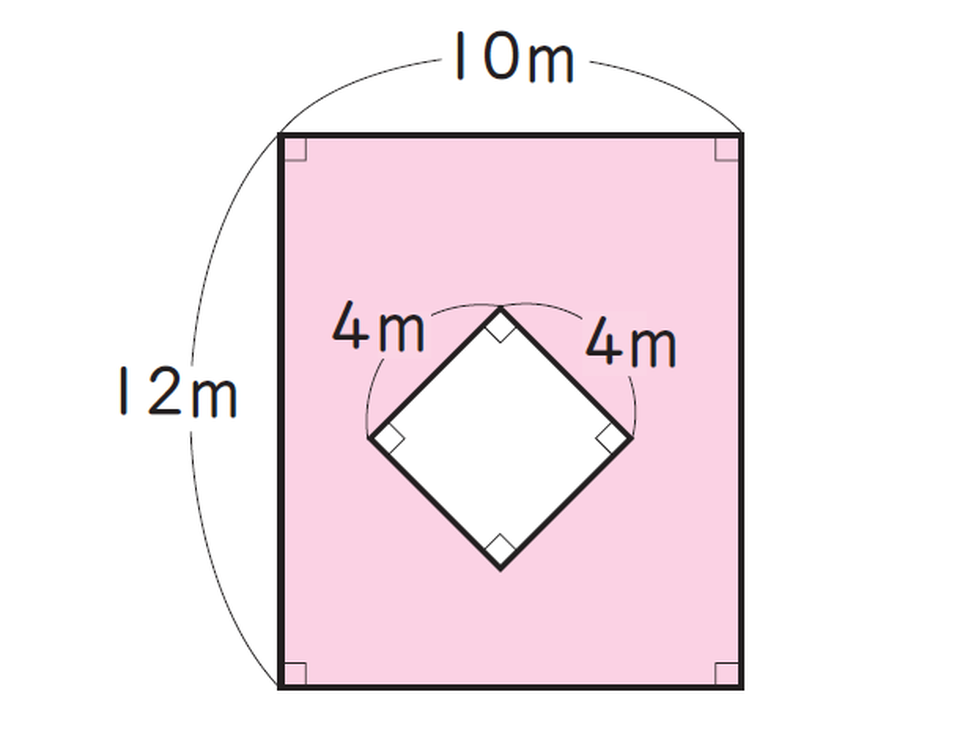
次の図形の、色がついた部分の面積を求めましょう。
<式>
12×10-4×4=120-16=104
<答え>
104㎡
大きい長方形の面積から、中にある正方形の面積をひいて求めることができました。
<例題>
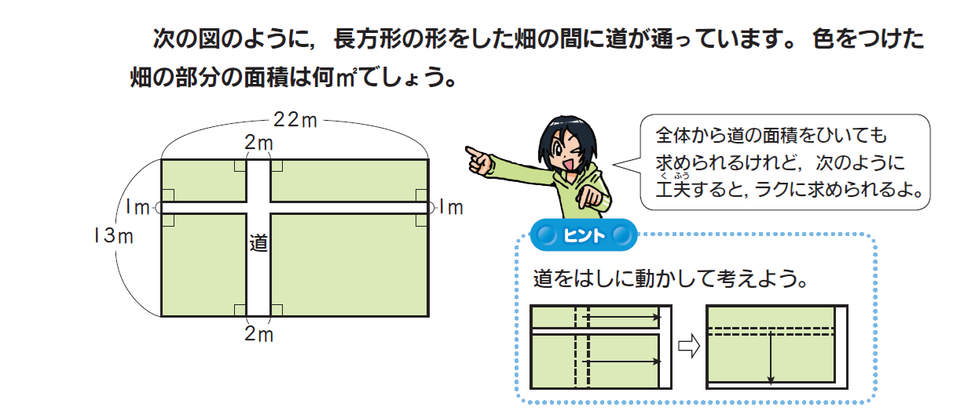
この問題の場合、道の部分の面積をひくよりも、ヒントにあるように、道をはしに動かして考えるほうが簡単です。
横の長さ22mから縦に走る道の幅2mをひいて20m、たての長さ13mから横に走る道の幅1mをひいて12mの長方形にして考え、公式にあてはめると、次のような式になります。
<式>
(22-2)×(13-1)=20×12=240
<答え>
240㎡
このような算数の応用問題に対応するには、家庭学習が欠かせません。算数の理解を深めるには、「進研ゼミ小学講座」の「チャレンジタッチ」がおすすめです。アニメーションや動画を使った解説で、遊び感覚で算数にふれることができ、理解が定着。忙しいおうちのかたに代わって、お子さまの学習を強力サポートします。
長方形の面積と横の長さがわかっている場合のたての長さの求め方
長方形の面積の発展問題では、面積と横の長さがわかっている長方形の、たての長さを求める問題でつまずくお子さまも少なくありません。
長方形の面積と横の長さがわかっているときは、公式にあてはめて、たての長さを求めることができます。次の例題で考えてみましょう。
<例題>
面積が30cm²で、横の長さが5cmの長方形があります。この長方形のたての長さは何cmでしょう?
まず、求める「たての長さ」を□cmとし、面積の公式にあてはめます。
<公式>
たて×横=長方形の面積
□×5=30
次に、□にあてはまる数字を考えます。
□は、30÷5で求められるので、□=6です。
たての長さは6cmとなります。
<答え>
6cm
このように、わからない長さを□㎝とおいて、面積を求める式にあてはめ、□を求めるという順序で解くと、文章題や応用問題でも迷わず解けるようになります。
<例題>
面積が100cm²で,たての長さが5cmの長方形の形をした鉄板があります。この鉄板の横の長さは何cmでしょう。
この場合も同様に、求める「横の長さ」を□cmとして公式にあてはめます。
<公式>
たて×横=長方形の面積
5×□=100
□=100÷5=20で、答えは20cmとなります。
<答え>
20cm
面積問題のつまずき克服には「チャレンジタッチ」がぴったり
算数の面積問題は、公式を覚えていても「どの長さをかけるのかがわからない」「逆算になると混乱する」といった理由で、苦手意識をもつお子さまが少なくありません。特に、面積からたてや横の長さを求める問題や、単位をそろえる計算は、つまずきやすいポイントです。
そのようなときに頼りになるのが、「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」です。「チャレンジタッチ」では、図やアニメーションを使ったレッスンで、面積を求める図形問題など、イメージしにくい単元も目で見て理解できます。さらに、間違えた問題はすぐに解き直しができる仕組みがあり、苦手をその場で解消できるのも魅力です。
教科書対応だから家庭学習もスムーズ。勉強が「わからない」「面倒」と感じるお子さまでも、自然に学習習慣が身につきます。お子さまの算数の苦手克服に、「チャレンジタッチ」での体験学習をぜひ取り入れてみてください。
- ここでご紹介している教材・サービスは2026年1月現在の情報です。教材ラインナップ・デザイン・名称・内容・お届け月などは変わることがあります。