- 学習法
容積とは?
体積との違いや求め方をわかりやすく解説

容積は、箱や容器の中にものがどれだけ入るかを表す大きさです。小学5年生で習う内容となっていますが、単位の換算や立体のとらえ方に悩むことも多いのではないでしょうか。
この記事では、容積と体積の違いをはじめ、容積の計算方法、応用的な問題の例までを解説します。
<目次>
容積とは?体積との違いは?
容積と体積は、どちらも大きさを表す言葉ですが、意味や使い方には明確な違いがあります。日常生活の中でも使われることがあり、区別して理解することが大切です。
ここでは、以下のような容積と体積の定義や、どのような場面で使い分けられるかについて解説します。
<容積とは?>
- 容積とは容器の中にものがどれだけ入るかを表す大きさ
- 容積と体積の違い
容積とは容器の中にものがどれだけ入るかを表す大きさ
容積とは、入れ物の中に水などがどれだけ入るかを表す大きさです。例えば、水そうやペットボトルのような容器には、決まった量の水やジュースが入りますが、この容器の中の空間が容積です。
容積を求める際は、直方体や立方体であれば「縦×横×高さ」で計算され、単位には「cm³(立方センチメートル)」「m³(立方メートル)」「L(リットル)」が使われます。
容積と体積の違い
学習過程において、容積と体積はだいたい同じタイミングで習うことになりますが、どのような違いがあるのでしょうか。2つの違いをまとめた内容が、以下の表になります。
■容積と体積の意味の違い
| 意味 | 使われる場面 | |
|---|---|---|
| 容積 | 入れ物の中にどれだけ入るかを表す大きさ | 水そうやペットボトルなどの液体や気体などが入る空間の大きさ |
| 体積 | ものの大きさ | 水そうやペットボトルなどもの自体の大きさ |
まず体積とは、ものの大きさのことです。水が入っている水そうやペットボトルなどであれば、容器全体のサイズを指します。体積を求める際は容積と同じく、直方体や立方体であれば「縦×横×高さ」で計算され、単位も「cm³(立方センチメートル)」や「m³(立方メートル)」を使用します。
つまり、容積と体積の関係をわかりやすく考えると、入れ物全体の大きさが体積で、ものが入る中の空間の大きさが容積です。ここで大切なのが、例えば、外側の大きさが同じ入れ物(体積が同じ)でも、内側の広さが狭ければ水が入る空間は小さくなります(容積が少なくなる)。つまり、体積が同じでも、容積は変わる場合もあることがわかります。
体積や容積のように、量や立体の構造を考える学習は、イメージがつかみにくく、つまずきやすい単元のひとつです。「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」なら、図やアニメーションを使ったわかりやすいレッスンで、視覚的に理解できる工夫が取り入れられています。
容積の単位と計算方法
次に、容積に使われる単位と、基本的な計算方法について見ていきましょう。容積に関して、小学校の算数では「cm³(立方センチメートル)」「m³(立方メートル)」「L(リットル)」といった単位が使われます。
直方体や立方体の容積は、「縦×横×高さ」で求めるのが基本の考え方です。例えば、以下のような、縦10cm、横10cm、高さ10cmの立方体の容積は、10×10×10=1000(cm³)となります。
■縦10cm・横10cm・高さ10cmの立方体

また、1L=1000cm³、1L=1000mlという単位の変換も覚えておく必要があります。身近な例では、お店で売っている1Lの紙パックのジュースは、パッケージに1000mlと書いてあることが多いでしょう。1L=1000mlということです。生活の中で見かけるものと単位を結びつけて考えることで、容積のイメージがつかみやすくなるかもしれません。
なお、計算時には長さの単位をそろえることも大切です。例えば、縦が10cm、横が50mm、高さが10cmのように単位が混ざっている場合は、すべて同じ単位に統一してから計算をする必要があります。
容積を求める問題例
次に、容積を求める具体的な問題の例を見ていきましょう。
<例題>
直方体の形をした入れ物を作りました。入れ物は、内のりの縦6cm、内のりの横10cm、深さ8cmです。この入れ物に、水が何cm³入るか求めましょう。
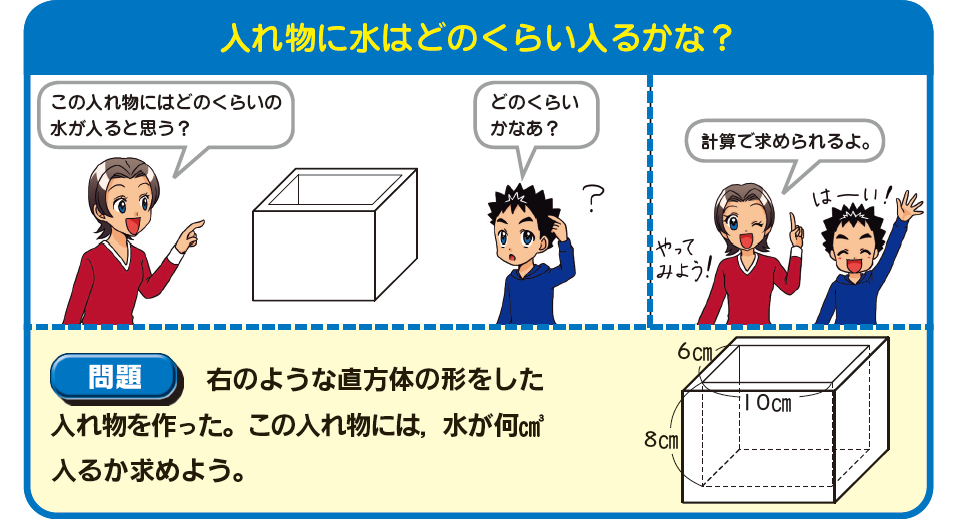
容積の問題に出てくる言葉で、入れ物の内側の長さを「内のり」、内側の高さのことを「深さ」といいます。直方体は、「縦×横×高さ」の計算式で求められますが、この場合は「内のりの縦×内のりの横×深さ」で計算をする必要があります。
<答え>
6×10×8=480(cm³)
こんな場合はどう計算する?容積に関する練習問題
容積の基本的な計算問題に加えて、単位を変換する問題や、水の体積から深さを求める応用問題などが出てくると、急に難しさを感じてしまうかもしれません。ただし、落ち着いて計算をしていけば、正しく答えを導くことができます。次に、容積の練習問題を見ていきましょう。
<問題1>
厚さ1cmの板を使って、直方体の形をした水そうを作りました。内のりの縦は50cm、内のりの横は70cm、深さは40cmです。この水そうの容積は何Lか求めましょう。
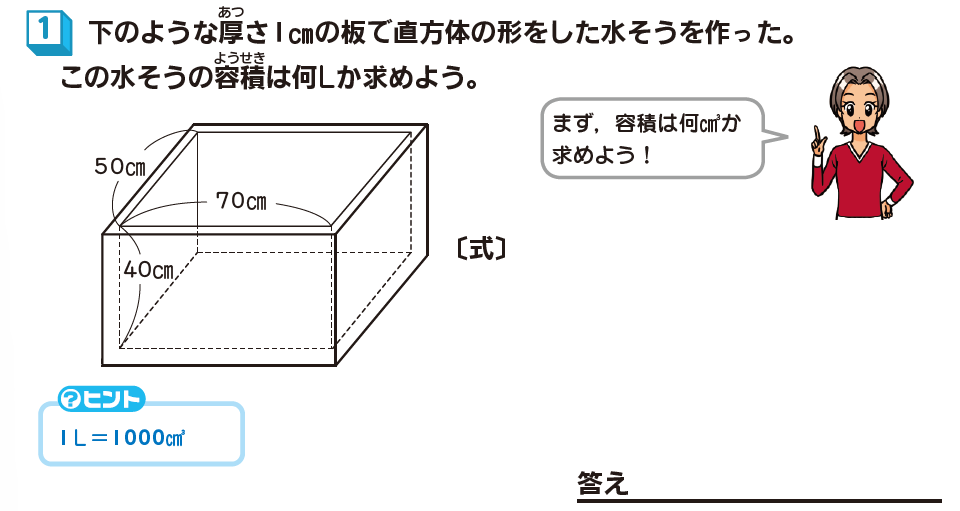
何Lか直接求める計算式はないため、この問題は2段階で解く必要があります。まず何cm³単位で求めて、次にL単位に直す方法です。内のりの縦は50cm、内のりの横は70cm、深さは40cmなので、容積は50×70×40=140000(cm³)となります。
次に、L単位に換算します。1L=1000cm³なので、140000÷1000=140(L)と計算できます。
<答え>
140L
水そうのサイズはcmで表されていますが、聞かれている容積の単位はLのため、単位換算を忘れないように注意が必要です。次は、水の深さを求める問題を見ていきます。
<問題2>
直方体の形をした水そうに、40kLの水を入れました。水そうは、内のりの縦4m、内のりの横5m、深さ3mです。このとき、水の深さは何mになるか求めましょう。
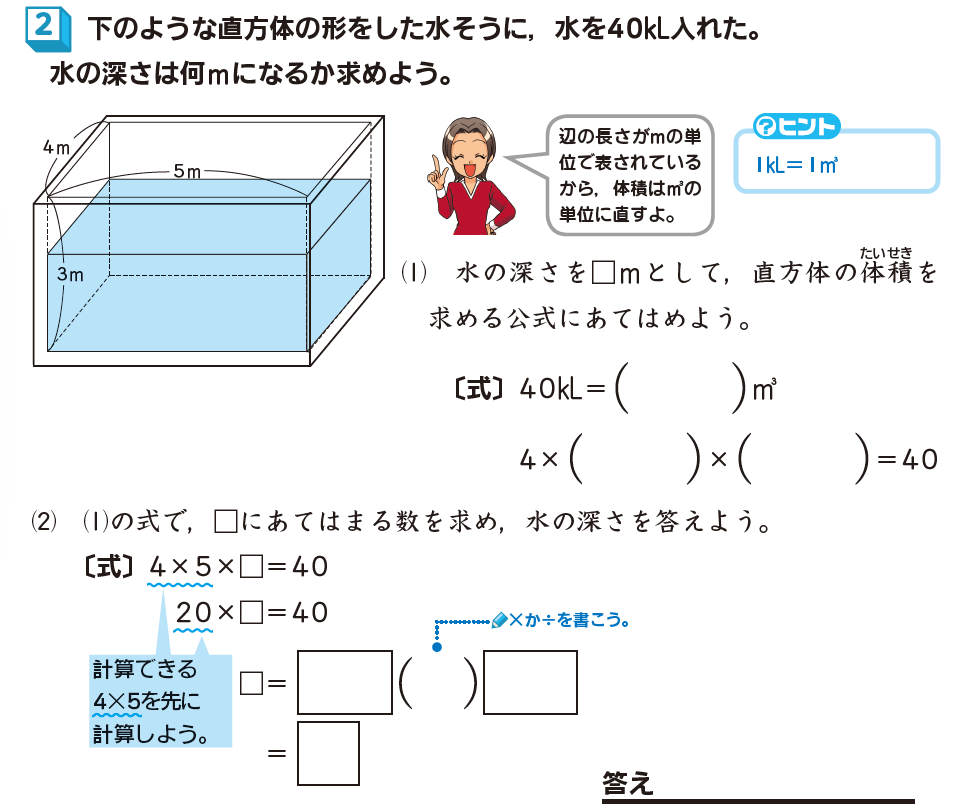
まず、kL(キロリットル)の単位のままでは計算できないので、単位を直します。1kL=1m³なので、水40kL=40m³となります。この問題のように、公式のうちの1つの数がわからないときは、わからない数を□として公式にあてはめて解くのが一般的です。
この問題では水の深さを□mとします。すると問題の場面は、4×5×□=40という式に表すことができます。
4×5を先に計算して、20×□=40となり、40÷20=2で□にあてはまる数は2となります。
<答え>
2m
水の体積から深さを逆算する問題は、一見すると難しく、悩んでしまうかもしれません。しかし、ここで使っている公式は、体積を求める基本的な公式と同じです。算数はいずれも基礎をしっかりと理解して問題練習をくり返すことで、落ち着いてまちがいなく問題を解くことができるようになるでしょう。
苦手な教科も、目で見て理解ができる「進研ゼミ小学講座」がおすすめ
容積や体積などの内容は、ものの大きさや空間を数値で表すため、感覚でとらえるのが難しい学習内容のひとつです。単位の変換、計算方法、図形のイメージなど、小学生にとってはつまずきやすいポイントといえるでしょう。
苦手な教科や単元がある場合におすすめなのが、「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」です。
「チャレンジタッチ」では、容積や体積のようにイメージしづらい内容も、図解や実例を活用したレッスンで、視覚的に理解できる教材となっています。また、苦手な問題の解き直しを行う仕組みや、学習習慣を定着させる工夫も充実。教科書に対応した内容で無理なく学習でき、自然と理解が深まります。
勉強が「わからない」「苦手」という気持ちに寄り添いながら、確かな理解につなげる「進研ゼミ小学講座」を、ぜひ活用してみてはいかがでしょうか。
- ここでご紹介している教材・サービスは2026年1月現在の情報です。教材ラインナップ・デザイン・名称・内容・お届け月などは変わることがあります。