倍数とは？
約数との違いと活用例を解説

倍数とはある整数を整数倍してできる数のこと

倍数とは、ある整数を整数倍してできる数のことです。例えば「2の倍数」は2、4、6、8、…です。これは、2という数に2×1、2×2、2×3、2×4、…と、整数を順番にかけた結果として現れる数で、限りなくあります。「3の倍数」なら、3×1、3×2、3×3、3×4、…という計算になるため、3、6、9、12、…の結果になります。

「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」なら、倍数のようにイメージしにくい学習内容も、視覚的にわかりやすく解説。ゲーム感覚で取り組める教材も充実しており、つまずきやすい算数も楽しく学べます。

約数とはある整数をわりきることのできる整数のこと

約数とは、ある整数をわりきることができる整数のことです。例えば「12の約数」は、12をわりきることのできる整数として、1、2、3、4、6、12の6つが挙げられ、このほかにはありません。このように、特定の数をわりきることができるかどうかを確かめながら、すべての約数を見つけていくことができます。

公倍数と公約数はどんな数？

小学校では倍数や約数といっしょに、「公倍数」や「公約数」も習うことになります。どちらも2つ以上の数に共通な性質をもった数ですが、意味や求め方には違いがあります。ここでは、それぞれの考え方について見ていきましょう。

公倍数と最小公倍数

公倍数とは、2つ以上の整数に共通な倍数のことです。例えば、3の倍数にも4の倍数にもなっている数を3と4の公倍数といいます。3の倍数は3、6、9、12、15、…と続き、4の倍数は4、8、12、16、20、…と続きます。2つの数字の倍数を並べて見ていくと、3と4に共通して現れる倍数は12、24、36、…です。この共通な倍数のことを、公倍数といいます。

■3と4の公倍数・最小公倍数

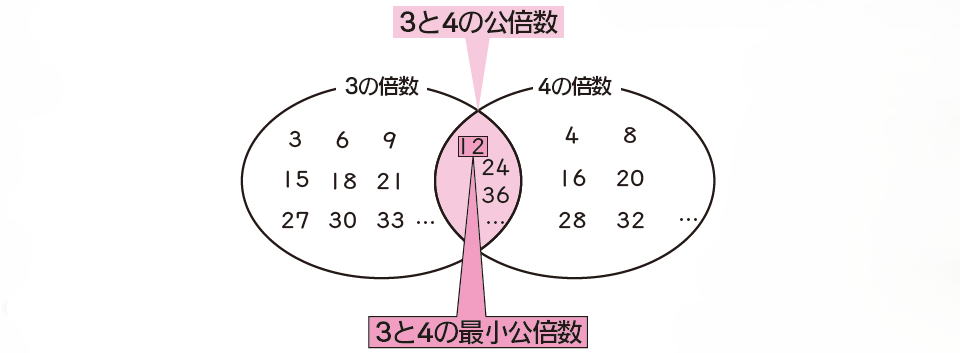
また、公倍数の中で一番小さい数を最小公倍数といいます。3と4の場合は12が最小公倍数です。

小学校の勉強では、倍数と約数の言葉に迷うこともあるかもしれませんが、倍数はどこまでも続いていく数で、最大という概念がありません。そのため、倍数や約数の問題で「一番小さい」「できるだけ小さい」のような語句が出てきたら、最小公倍数を求める問題だと推測できるでしょう。

公約数と最大公約数

公約数とは、2つ以上の整数をわりきることのできる共通な約数のことです。例えば、12と16の場合、12の約数にも16の約数にもなっている数を、12と16の公約数といいます。12の約数は1、2、3、4、6、12で、16の約数は1、2、4、8、16です。2つの約数を並べてみると、どちらの数もわりきることのできる共通の約数は1、2、4であることがわかり、これらが12と16の公約数となります。

■12と16の公約数・最大公約数

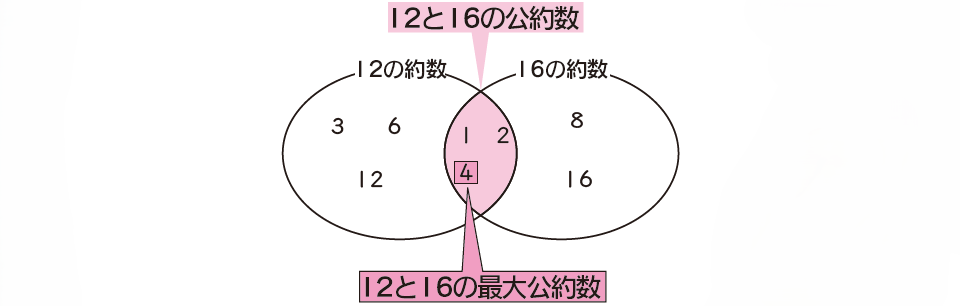
また、公約数の中で一番大きい数を最大公約数といいます。12と16の場合は4が最大公約数です。
約数は倍数と異なり、ある整数をわりきることのできる整数を指すので、数に限りがあります。そのため、小学校で出てくる倍数や約数の問題文に「一番大きい」「できるだけ大きい」などの語句があれば、最大公約数を求める問題だと考えることができるでしょう。

勉強だけでなく生活の中で役立つ倍数と約数

倍数や約数の考え方は、学校の勉強はもちろんのこと、日常生活でも役立ちます。ここでは、倍数を使う場面と、約数を使う場面の例をそれぞれ見ていきましょう。

倍数を使う例

まずは、日常で倍数を使う例を考えます。例えば、パンにコロッケを挟んでコロッケパンを作る予定で、お店で買い物をするとしましょう。お店では、1袋3個入りのパンと、1袋4個入りのコロッケを売っています。パンとコロッケどちらかが余ってしまわないように、ぴったりの数でコロッケパンを作るには、少なくともそれぞれ何袋ずつ買えばよいでしょうか。

ここでは倍数の考え方を使います。今回は1袋3個入りのパンと、1袋4個入りのコロッケのため、3と4の公倍数を考えます。以下は、それぞれの倍数を並べた表です。

■3の倍数と4の倍数

3と4の倍数から、2つの数の公倍数を考えます。パンとコロッケの数が等しくなるのは、最初は12だということがわかります。

つまり、コロッケパンの個数は12個とわかり、パンの袋は4袋（12÷3）、コロッケの袋は3袋（12÷4）が必要です。

約数を使う例

次に、日常で約数を使う例を考えてみましょう。例えば、16個のクッキーが手元にあり、同じ数ずつ余りなく分けたいとします。この場合、まず何人で分ければクッキーが余らないかを考える必要があります。

ここで出てくるのが、16をわりきることのできる数、つまり16の約数です。16の約数は、1、2、4、8、16になります。2人で分ければ1人8個ずつ配ることができ、4人で分ければ1人4個ずつ、8人で分ければ1人2個ずつ、16人で分ければ1人1個ずつとなり、どの場合もクッキーは余りなく分けることができます。

このように、日常のちょっとした場面でも、倍数や約数の考え方が役立つことがあります。小学校で習う算数が、ただの計算問題というだけでなく、自分の身近な生活にもつながっていることがわかれば、子どもたちもより楽しく、興味をもって学ぶことができるかもしれません。

苦手な教科も、くり返しわかりやすく取り組める「進研ゼミ小学講座」がおすすめ

倍数や約数は、言葉の意味や求め方で少し迷う内容ではありますが、身近な例や図を使って考えることで、より理解しやすくなります。特に小学校の算数は、学年が進むにつれて内容が複雑になるため、苦手な部分をそのままにして次に進むのではなく、その都度しっかりと理解を積み重ねていくことが大切です。

「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」は、学習で悩みがちなポイントをおさえながら、お子さまが自然と学びたくなる工夫がたくさん取り入れられています。
例えば算数は、図やアニメーションを使った説明で、倍数や約数の考え方も目で見て理解できます。また、計算をゲーム感覚で楽しく学べる教材も充実しているため、自分でどんどん進めることができます。
さらに、間違えた問題の解き直しや、つまずきの原因を自動判定するシステムも搭載されており、苦手をそのままにせず、解消していくことが可能です。

楽しさとわかりやすさを両立させた「進研ゼミ小学講座」で、算数の苦手意識を自信に変えていきましょう。