約数とは？小学生にも
わかりやすい学習サポート術

小学生が「約数」でつまずきやすい理由

「約数」は小学校5年生で初めて登場する単元で、つまずきやすい単元の1つです。その主な理由は、次の2つです。

算数的な用語に慣れておらず、言葉の意味で混乱しやすい

「約数」「倍数」「公約数」「公倍数」など、似た用語が一度に登場するため、それぞれの意味を正確に理解するのが難しく、混同してしまうことがあります。

わり算・かけ算の基礎があいまいなまま応用に進んでしまう

約数はある整数をわりきることができる整数という性質をもつため、かけ算やわり算の理解が不十分な状態では、正しく求めることができません。とくに文章題では、その傾向が顕著です。

こうした理由から、約数でつまずかないためには、用語の理解や基礎の確認が重要です。

約数とは？意味と求め方をわかりやすく解説

約数とは、ある整数をわりきることができる整数のことを指します。これは、わり算をしたときにあまりが出ずにぴったりわりきれる数という意味です。例えば、12の約数は「1、2、3、4、6、12」です。実際にわってみると、すべてきれいにわりきれることがわかります。

一方で、12÷5=2.4のように、商が小数になる場合はわりきれても約数ではありません。必ず商が整数になってわりきれる数が約数です。

約数を見つけるポイント

約数を見つけるときには、次のような性質や考え方を押さえておくとスムーズに進められます。

「1」とその数自身は必ず約数になる

どんな整数も、「1」とその数自身ではわりきれるため、必ずこの2つは約数に含まれます。先ほどの12でも、1と12は約数でした。

約数の個数には限りがある

倍数はかけ算で求めるのでどこまでも続きますが、約数の個数は有限です。ある整数に対して、いくつかしか存在しません。

かけ算の式で考える

約数は、基本的にはわり算でわりきれる数を探して求めます。例えば、「12」の約数を求めるときは、「12÷1」「12÷2」…というように1から順にわっていき、あまりが出ないものを見つけますが、この方法だと数が大きくなったとき、時間がかかってしまいます。そこで、かけ算の式で考える方法をご紹介しましょう。例えば、「1×12」「2×6」「3×4」など、積が「12」になるような組を探すと、見落としなく約数を求めることができます。

実際に見て理解する

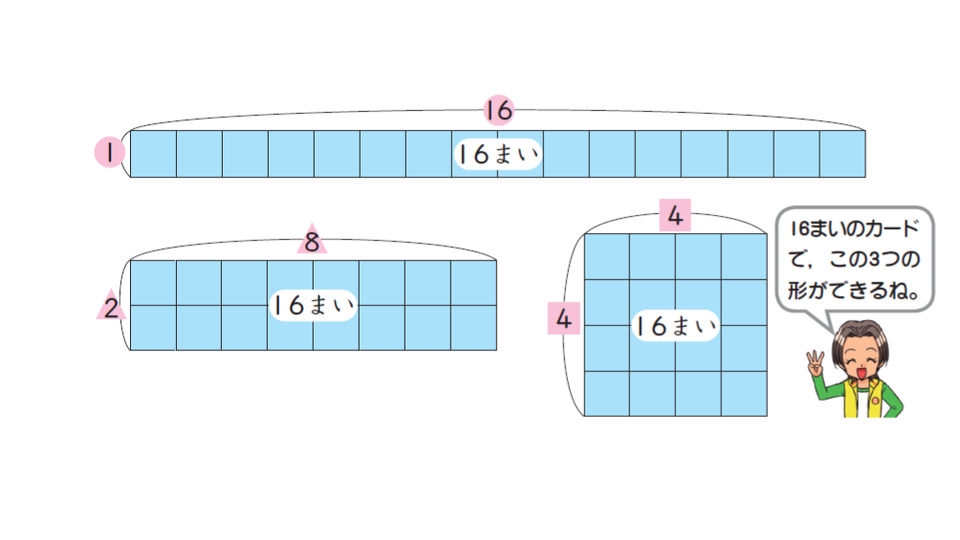
同じ大きさの正方形のカードを使って目で見て理解するのも効果的です。ある枚数のカードで長方形や正方形の形を作るとき、たてやよこに並べる数は、その数の約数にあたります。「あまりなくわりきれる」という意味を、視覚的にとらえられます。

約数を利用する場面

約数は、ある整数をわりきることができる整数のことを指します。例えば、「16」の約数を求める場合、「16÷□＝整数」となるときの□が「16」の約数です。以下の例題で確認してみましょう。

「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」では、間違えた問題を繰り返し復習できるため、つまずきやすい単元でも、理解を深めながら無理なく習得できます。

詳しくは以下より無料体験教材と資料を請求してみてください。

家庭でできる学習サポート

ここでは、学校で学ぶ「約数」の考え方を、家庭でも無理なく身につけられる方法をご紹介します。

日常生活の中で約数にふれる機会をつくる

「約数」は、日常生活の中でも体験できます。例えば、お菓子を配るときに「何人だと同じ数ずつ分けられるかな？」と問いかけることで、「わりきることができる数＝約数」という感覚が自然と身につきます。また、「1人分の数×人数＝全体の数」という式に気づくことで、かけ算とわり算の関係も理解しやすくなります。無理に教え込まず、生活の中で自然に声かけをすることが理解を深めるポイントです。

問題演習の習慣をつくる

日常生活での体験は、約数の考え方を理解する入り口としてとても有効です。ただし、学んだことをしっかり定着させるには、問題演習による反復練習も欠かせません。 タブレット学習や市販の問題集を活用することで、日常体験で得た感覚を知識として身につけることができます。特に「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」は、間違えた問題を自動で復習に組み込む仕組みがあるため、苦手を放置せずに着実に克服できるのが特長です。

約数の理解は、算数の土台をつくる大切なステップ

約数は、算数の基礎として非常に重要な単元です。倍数や公約数、最小公倍数といった似た用語とあわせて整理することで、より深い理解につながります。
忙しいご家庭でも、日常の声かけやタブレット学習を取り入れることで、無理なく学習をサポートすることが可能です。「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」なら、自宅でくり返し学べる仕組みで、つまずきやすい単元も着実に定着します。ぜひ入会をご検討ください。