- 学習法
割合とは?算数が苦手な小学生に
わかりやすく教える方法を解説

小学校の算数の中でも「割合」は、苦手に感じるお子さまが多い単元のひとつです。「比べられる量」と「もとにする量」の区別がつかないなど、割合の基本的な考え方でつまずいてしまうケースも少なくありません。しかし割合は、中学校以降の学習にもつながり、中学1年生では「文字式」「方程式」の単元で必要となってきます。小学生のうちに基礎を固めておくことが大切です。
この記事では、割合の基本的な考え方や、つまずきやすいポイント、身近な例を使った理解のコツについて詳しく解説します。お子さまの割合の学習に不安を感じている保護者のかたは、ぜひ参考にしてください。
<目次>
割合とは?簡単な例から理解しよう
割合とは、もとにする量を1とみたとき、くらべられる量がどれだけにあたるかを表した数のことです。割合の表し方には小数、分数、倍、百分率、歩合などほかにもありますが、倍を用いて捉えると、シンプルでわかりやすくなります。
例えば、500円だったおこづかいが1000円になったなら、500円をもとにすると1000円の割合は2倍です。1000円だったおこづかいが500円になったなら、1000円をもとにすると500円の割合は0.5倍になります。このように、もとになる量に対して何倍になっているかを表すと捉えれば、考えやすくなります。
野球の打率やお店のセール品の割引率など、割合は私たちの身近なところにたくさんあります。まずはこのような簡単な例で、割合の考え方を理解するところから始めましょう。
割合のつまずきポイント1:「比べられる量」と「もとにする量」の区別がつかない
500円だったおこづかいが1000円になったとき、500円をもとにすると1000円の割合が1000÷500=2(倍)となるように、割合は、「比べられる量÷もとにする量」で求められます。しかし、問題文を読んだときに、「比べられる量」と「もとにする量」の区別がつかなくなり、反対にしてしまう間違いがよく見られます。「割合=比べられる量÷もとにする量」という計算式を覚えていても、それぞれを正しく区別できなければ、式が立てられません。
まずは、もとにする量がどれなのかを意識して考えることが、区別するためのポイントです。やさしい問題で、もとにする量を見つける練習から始めてみましょう。
<もとにする量の見つけ方>
「~に対して」「~をもとにして」などの言葉があるときは、「~」の部分が、もとにする量となります。また、「~の〇倍」「~の〇%」「~の〇割」のように割合の前に「の」があるときは、「の」の前にある部分が「もとにする量」です。
<例題>
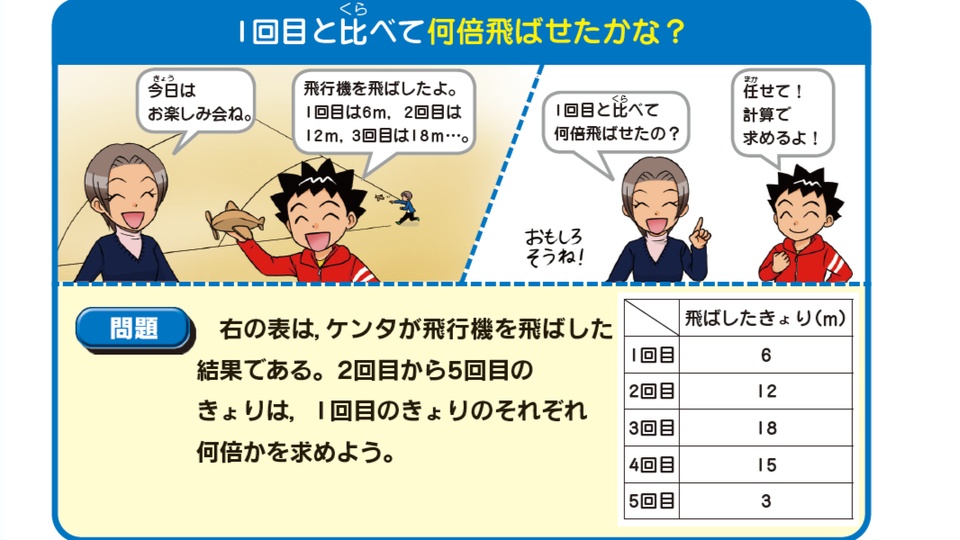
ケンタが飛行機を飛ばしてきょりを測ったところ、1回目は6m、2回目は12m、3回目は18m、4回目は15m、5回目は3mという結果でした。2回目から5回目のきょりは、1回目のきょりのそれぞれ何倍ですか?
「1回目のきょりの何倍か?」なので、もとにする量は1回目のきょりだとわかります。もとにする量がわかれば、「割合=比べられる量÷もとにする量」の計算式にあてはめるだけです。
<答え>
2回目:12÷6=2で割合は2倍
3回目:18÷6=3で割合は3倍
4回目:15÷6=2.5で割合は2.5倍
5回目:3÷6=0.5で割合は0.5倍
5回目のきょり(3m)のように、もとにする量の1回目のきょり(6m)より、比べられる量のほうが数量が小さくなることもあります。数字の大小に惑わされずに、比べられる量ともとにする量を区別して式を立てましょう。
割合のつまずきポイント2:分数や小数の計算が出てくる
割合つまずきポイント1の「飛行機を飛ばしたきょり」の問題で、4回目のきょりの割合が、15÷6=2.5で2.5倍となったように、割合の問題では、答えが整数にならない問題もよく出てきます。せっかくもとにする量を正しく区別できても、整数にならなかったり、小数の筆算をしてもわり切れなかったりすることで、間違えたと判断して途中でやめてしまうお子さまも少なくありません。
こうした場合は、割合は整数にならないこともよくあり、もし割り切れないときは分数で表すことを伝え、割合の前提となる分数や小数の計算を復習することが、苦手克服に効果的です。
「進研ゼミ小学講座」のタブレット教材「チャレンジタッチ」なら、お子さまの学習レベルに応じて、学年をさかのぼって復習したり、先の内容にチャレンジしたりできます。苦手な単元は、基礎からじっくり学び直すことで、自信を持って取り組めるようになります。
割合の表し方「百分率(パーセント)」と「歩合(割・分・厘)」
割合を表すときには、「百分率(パーセント)」や「歩合(割・分・厘)」がよく使われます。「小数で表した割合を百分率・歩合で表そう」など、問題文に出てくることもある用語なので、それぞれの言葉と考え方を覚えておくことが大切です。ここでは、百分率と歩合の基本的な考え方をご紹介します。
百分率(パーセント)
「1回目のきょりが6mのとき、2回目のきょりの12mは、1回目のきょりの何倍ですか?」という問題で、答えが「2倍」となるように、何倍かを計算するときは、もとにする量の6mを「1」として考えていました。
このもとにする量を、1ではなく100として考えるのが、百分率(パーセント)です。1を100として考えるため、計算上は、小数で表された割合に100をかければ百分率で表された割合になり、1が100%、0.1が10%、0.01が1%になります。
歩合(割・分・厘)
もう1つ、割合を表す単位として歩合があります。割合を表す1が10割、0.1が1割、0.01が1分、0.001が1厘になります。割合の表し方を整理すると、次のようになります。
■割合の表し方
| 小数 | 1 | 0.5 | 0.25 | 0.1 | 0.01 | 0.001 |
|---|---|---|---|---|---|---|
| 百分率 | 100% | 50% | 25% | 10% | 1% | 0.1% |
| 歩合 | 10割 | 5割 | 2割5分 | 1割 | 1分 | 1厘 |

<例題>
お楽しみ会で出ている店は全体で50店、そのうち、食べ物を売る店は26店です。食べ物を売る店の数は全体の店の数のどれだけの割合ですか?
この問題の場合、もとにする量は「50店」です。「~の数は~の数のどれだけの割合?」という問題文の場合、後にでてくる「~の数の」のほうが、もとにする量になります。
「割合=比べられる量÷もとにする量」にあてはめると、26÷50=0.52で、割合を小数で表すと0.52となります。問題文が「食べ物を売る店の数は全体の店の数のどれだけの割合か、百分率で答えましょう。」なら、0.52に100をかけて答えは52%。問題文が「食べ物を売る店の数は全体の店の数のどれだけの割合か、歩合で表しましょう。」なら、0.52の0.5は5割、0.02は2分なので、答えは5割2分と表します。
割合の問題を解くコツは?「もとにする量」を見つけて図で整理
割合の問題を解くコツとして、問題文を図で整理するという方法があります。例題をもとに、図のかき方を紹介します。

<例題>
ケンタのクラスは30人で、お楽しみ会の参加者はクラス全体の人数の0.7の割合でした。参加者は何人ですか?
割合の問題を図で整理するときはまず、もとにする量を見つけます。この問題の場合、「全体の人数の0.7の割合」とあり、割合0.7の前の「の」の前の言葉、つまり「全体の人数」がもとにする量だとわかるので、もとにする量は「30人」です。もとにする量である30人を1とし、問題文を数直線の図で表すと、次のようになります。
<図のかき方>
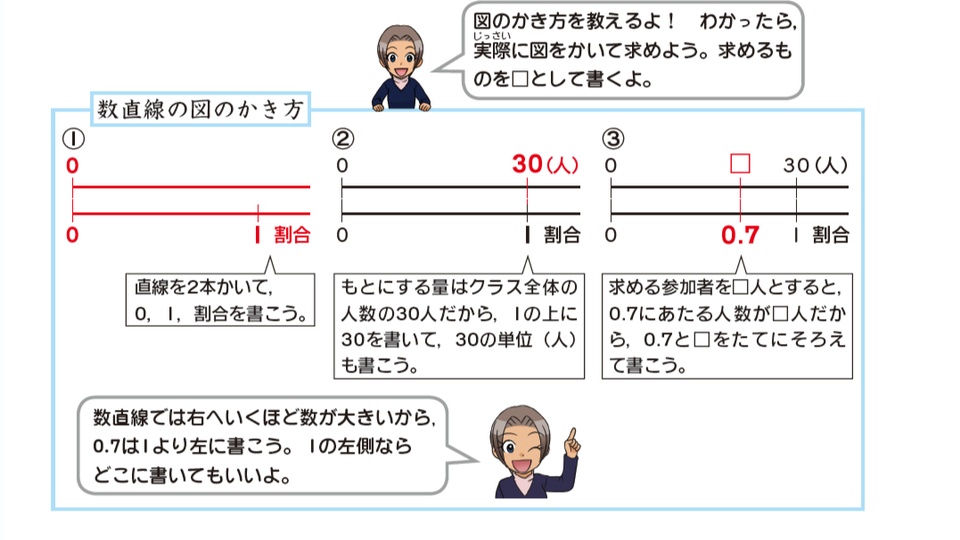
図から参加者の人数が、1の0.7倍(×0.7)であることが理解しやすくなり、30×0.7で参加者の人数を求められることがわかります。この問題の答えは、30×0.7=21で、21人です。
もちろん、比べられる量は「もとにする量×割合」で求めることができますが、「比べられる量=もとにする量×割合」という計算式を覚えていなくても、このように図をかくことで答えを求めることが可能です。
また、クラス全体の人数がわからず、「クラス全体の人数の0.7倍が21人です。クラス全体の人数は何人ですか。」という問題もあります。この場合は21÷0.7=30(人)と求めます。「もとにする量=比べられる量÷割合」という計算式です。こちらも、図をかくことで計算式を覚えていなくても問題を解くことができるでしょう。
身近なものから割合を考える
割合の理解を深めるには、お子さまが興味を持ちやすい身近な例を使うことが効果的です。スポーツが好きなお子さまなら、好きなチームの勝率をいっしょに計算してみましょう。野球チームが10試合中7試合に勝ち、3試合負けたなら、勝率は7÷10で0.7です。また、お子さま自身がスポーツをしているなら、シュートやキックの成功率を記録して割合で表してみるのもおすすめです。
お買い物の場面でも割合は活用できます。お子さまが欲しがっているゲームやおもちゃを例に、「◯◯円の商品が3割引だといくらになるかな?」など、いっしょに考えてみてください。また、スーパーで「◯%引き」のシールが貼られた商品を見つけて、値段を計算してみることも、割合の実用性を感じられる機会になります。

<例題>
シューティングゲームでマユは8回シュートして、6回入れました。入れた数はシュート数の何%ですか?
答えは、6÷8=0.75で75%です。親子でシュートの成功率を競うなど、割合の計算を遊びに取り入れてみると、割合の学習への興味が広がるかもしれません。
日常にある割合に気づくことで割合の理解を深めよう
割合は、小学校の算数の中でも難しく感じる単元のひとつですが、割合の考え方は身近な場面にも使われていて、理解を深めやすい分野でもあります。大切なのは、まずはやさしい問題から始めて、基本をしっかり身につけること。その第一歩として、「もとにする量」がどれかを問題文の中から見つけられるようになることがポイントです。
「進研ゼミ小学講座」は、お子さまの理解度に合わせて、基礎から無理なくステップアップできる教材です。家庭での学習でも、「わかった!」「できた!」という実感を持たせてあげたい保護者のかたにぴったりの内容となっています。割合の学習をしっかり基礎から身につけるためにも、「進研ゼミ小学講座」の入会を検討してみてはいかがでしょうか。
- ここでご紹介している教材・サービスは2026年2月現在の情報です。教材ラインナップ・デザイン・名称・内容・お届け月などは変わることがあります。